Интерполяционный полином Лагранжа

Будем искать функцию 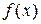в виде полинома заданной степени 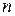– интерполяционного полинома, т. е. положим что

,

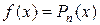где

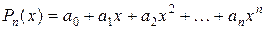(14.1)

и в соответствии с определением интерполирующей функции

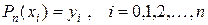(14.2)

Поскольку степень полинома известна, то поиск полинома сводится к нахождению набора его коэффициентов .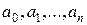

14.3.1 Определение коэффициентов интерполяционного
полинома

Воспользовавшись выражением (14.1) для искомого полинома 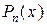и условием (14.2), получим систему линейных уравнений относительно неизвестных коэффициентов .

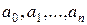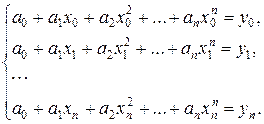(14.3)

Систему уравнений (14.3) представим в матричном виде, введя соответствующие обозначения.

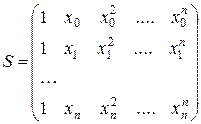
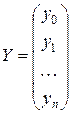
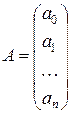
В результате система уравнений (14.3) приобретает вид

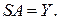(14.4)

Откуда

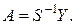(14.5)

Отметим, что задача интерполяции в описанной выше постановке имеет единственное решение. Это означает, что не существует двух различных наборов коэффициентов 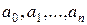, удовлетворяющих условию (14.2). Это следует из того, что искомые коэффициенты полинома определяются как решение системы линейных уравнений, имеющей единственное решение.

Французский математик Лагранж предложил способ построения интерполяционного полинома без предварительного вычисления коэффициентов 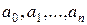, т. е. без решения системы уравнений (14.3).

Будем искать интерполяционный полином, который в данном случае обозначим через 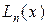, в виде

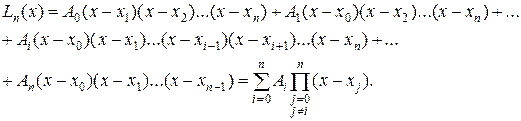(14.6)

Неизвестные коэффициенты 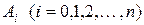определим из условия

.

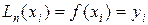Последовательно полагая 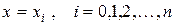, получим

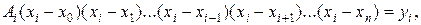
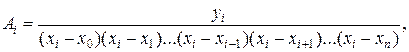
Подставляя найденные значения коэффициентов 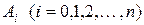в выражение (14.6) для многочлена 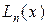, получим

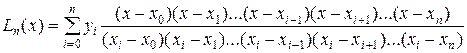(14.7)

Полученный таким образом полином называется интерполяционным полиномом Лагранжа.

Следует отметить, что полином Лагранжа 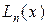просто представляет собой другую форму записи рассмотренного ранее полинома 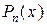, что следует из единственности решения задачи интерполяции.

Выражение для полинома Лагранжа 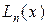может быть легко преобразовано к виду 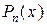путем группировки коэффициентов при соответствующих степенях аргумента .

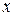Примеры.

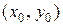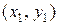Пусть имеем две точки и , что соответствует значению 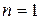. Тогда

.

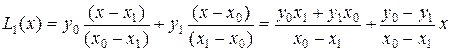Обозначая 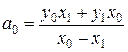и 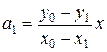, получаем

.

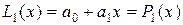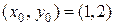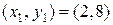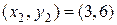Пусть имеем три точки , и , что соответствует значению 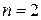. Тогда

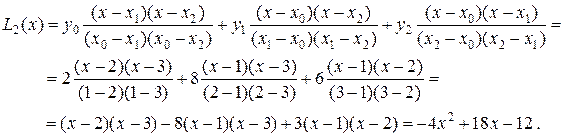
Достоинства полинома Лагранжа:

· график интерполяционного многочлена Лагранжа проходит через каждую точку массива;

· конструируемая функция легко описывается (число подлежащих определению коэффициентов интерполяционного многочлена Лагранжа на сетке 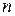равно);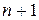

· построенная функция имеет непрерывные производные любого порядка;

· заданным массивом интерполяционный многочлен определен од­нозначно.

Недостатки полинома Лагранжа:

· степень интерполяционного многочлена Лагранжа зависит от числа узлов сетки, и чем больше это число, тем выше степень интерполяционного многочлена и, значит, тем больше требуется вычислений;

· изменение хотя бы одной точки в массиве требует полного пере­счета коэффициентов интерполяционного многочлена Лагранжа.