Компонентные уравнения реактивных элементов (емкостей и индуктивностей) описываются дифференциальными соотношениями. Для линейных и постоянных элементов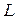 и
и 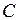 компонентные уравнения, как простейшие дифференциальные уравнения, преобразованием Лапласа трансформируются в алгебраические уравнения и наоборот. В результате соотношения из временного представления (относительно переменной
компонентные уравнения, как простейшие дифференциальные уравнения, преобразованием Лапласа трансформируются в алгебраические уравнения и наоборот. В результате соотношения из временного представления (относительно переменной 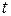 ) переводятся в комплексную плоскость переменной
) переводятся в комплексную плоскость переменной 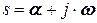 . При установившемся синусоидальном воздействии
. При установившемся синусоидальном воздействии 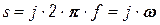 .
.
Применяя преобразование Лапласа к уравнению (3.12)
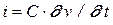 ,
,
получаем
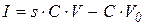 . (3.20)
. (3.20)
Преобразование Лапласа уравнения (3.17)
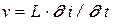
дает
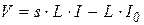 . (3.21)
. (3.21)
При нулевых начальных условиях 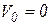 и
и 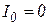

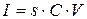 ; (3.22)
; (3.22)
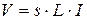 ; (3.23)
; (3.23)
откуда
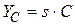 ; (3.24)
; (3.24)
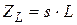 ; (3.25)
; (3.25)
либо
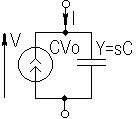
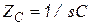 ; (3.26)
; (3.26)
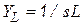 . (3.27)
. (3.27)
Перепишем уравнения (3.20) и (3.21) в виде
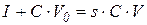 ; (3.28)
; (3.28)
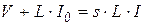 , (3.29)
, (3.29)
здесь 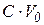 - источник тока, включенный параллельно
- источник тока, включенный параллельно 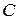 ;
; 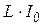 - источник напряжения, включенный последовательно с
- источник напряжения, включенный последовательно с 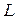 . Можно также записать уравнения (3.20) и (3.21) в виде
. Можно также записать уравнения (3.20) и (3.21) в виде
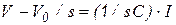 ; (3.30)
; (3.30)
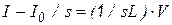 , (3.31)
, (3.31)
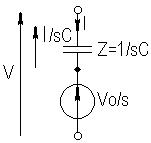
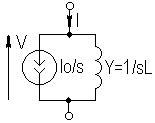
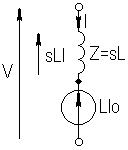
где 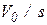 - источник напряжения, включенный последовательно с
- источник напряжения, включенный последовательно с 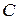 ;
; 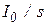 - источник тока, включенный параллельно с
- источник тока, включенный параллельно с 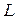 .
.
Рассмотренные представления удобно свести в таблицу 3.1.
Таблица 3.1 – Представление реактивных элементов
| Элемент | Проводимость | Сопротивление |
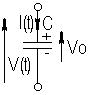
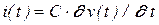
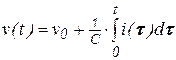
|
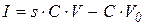
| 
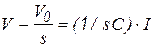
|
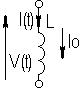
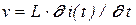
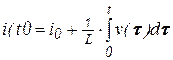
| 
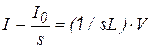
| 
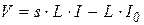
|
 2014-02-12
2014-02-12 710
710








