Табличный метод

ПРЯМЫЕ МЕТОДЫ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Идея табличного метода заключается в объединении топологических и компонентных уравнений цепи. В качестве топологических уравнений используются уравнения для токов и напряжений ветвей, выраженные через матрицу инциденций. При таком подходе все токи и напряжения ветвей и напряжения узлов рассматривается как неизвестные переменные. Этот метод, очевидно, является наиболее общим, однако приводит к системе уравнений высокого порядка.

Допустим, что цепь имеет 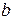ветвей и 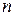независимых узлов, содержит R -, L -, C -элементы, зависимые и независимые источники и другие, часто используемые элементы. Топологические свойства цепи можно отобразить матрицами инциденций 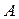, сечений 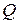, и контуров 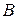. Т.к. матрица инциденций, в отличие от матриц сечений и контуров, формируется непосредственно по схеме, именно она используется в табличном методе. Уравнение Кирхгофа для токов, как известно, запишется в виде

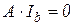. (4.1)

Напряжения ветвей связаны с напряжениями узлов как

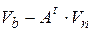, (4.2)

где 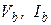- напряжения и токи ветвей; 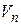- напряжения узлов.

Компонентные уравнения в самом общем случае могут быть записаны как

,

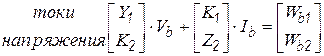где 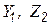- соответственно проводимость и импеданс; 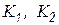– безразмерные константы; 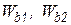- токи и напряжения независимых источников, в том числе источников, учитывающих влияние начальных условий на конденсаторах и катушках индуктивности. Для компактности воспользуемся более краткой формой компонентных уравнений

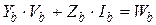. (4.3)

Заметим, что для различных типов ветве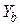й и 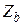могут принимать конкретное значение: +1, -1 либо 0, а 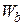- конкретное значение, либо 0.

В таблице 4.1 представлены значения 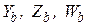для некоторых типов ветвей.

Таблица 4.1 – Компонентные уравнения двухполюсников

Элемент	Компонентные уравнения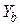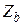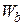
Резистор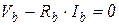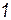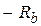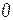
Проводимость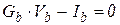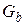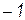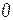
Конденсатор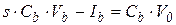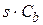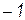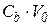
Катушка индуктивности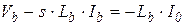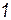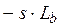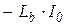
Источник напряжения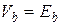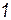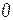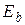
Источник тока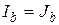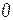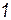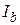

Заметим, что в таблице 4.1 конденсатор представлен как проводимость 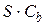, а индуктивность - как сопротивление .

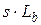В принципе, возможно и обратное представление, однако, забегая вперед, можно отметить, что для формального перехода от алгебраических уравнений в частотной области к дифференциальным уравнениям во временной области недопустимы множители типа .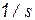

Таким образом, это ограничение необходимо соблюдать, если на основании математической модели предполагается вычисление временных характеристик путем перехода от алгебраических уравнений к дифференциальным уравнениям и их последующего интегрирования.

Табличную систему уравнений можно представить в виде

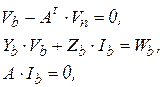(4.4)

или в блочной матричной форме

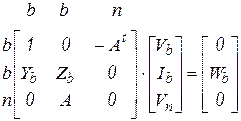, (4.5)

или в общем виде

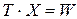. (4.6)

Как следует из структуры уравнений, блочная матрица 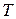имеет на главной диагонали квадратные матрицы. При табличном методе не различаются источники и пассивные компоненты, как в обобщенном узловом методе. Нумерация элементов также может быть произвольной.

В качестве примера рассмотрим цепь, изображенную на рис. 4.1.

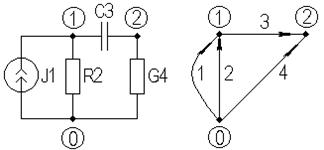
Рисунок 4.1 – Пассивная RC -цепь

Матрица инциденций схемы:

.

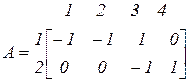Используя, матрицу инциденций схемы и таблицу 4.1 компонентных уравнений ветвей, в соответствии с (4.5) получаем следующую табличную систему

.

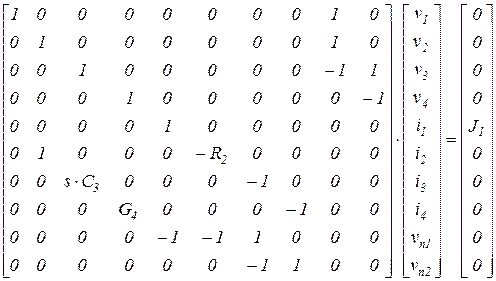Если в начальный момент времени на емкости 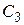есть напряжение 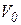, то седьмой элемент вектора источников равен .

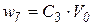В качестве достоинств табличного метода в сравнении с узловым либо контурным методами следует отметить возможность представления более широкого набора типов ветвей, а также возможность представления некоторых ветвей как в виде проводимости, так и в виде сопротивления. Управление представлением реактивных ветвей становится актуальным при расчете временных характеристик цепей с использованием преобразования Лапласа для перехода от алгебраических уравнений к дифференциальным и их последующим интегрированием.

В реальных схемах, кроме двухполюсных элементов, используются и более сложные элементы, например управляемые источники активных схем, поэтому расширим таблицу компонентных уравнений (таблица 4.2).

Таблица 4.2 – Компонентные уравнения идеальных элементов

Элемент	Обозначение	Компонентные уравнения
Разомкнутая цепь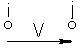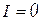
Короткозамкнутая цепь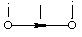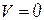
Источник тока, управляемый напряжением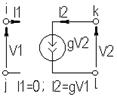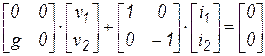
Источник напряжения, управляемый напряжением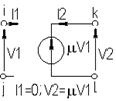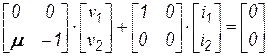
Источник тока, управляемый током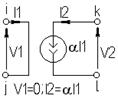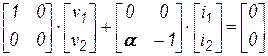
Источник, напряжения управляемый током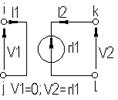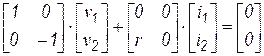
Операционный усилитель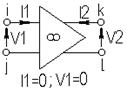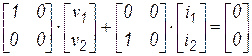

Для иллюстрации табличного метода в качестве примера рассмотрим схему рис. 4.2, содержащую источник напряжения, управляемый напряжением (ИНУН).

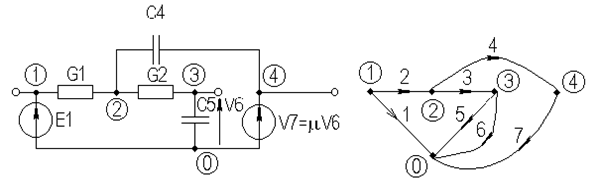
Рисунок 4.2 – Схема с источниками напряжения, управляемого напряжением

Ввиду громоздкости табличной матрицы запишем лишь матрицу инциденций

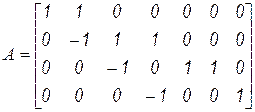
и компонентные уравнения рассматриваемой схемы

.

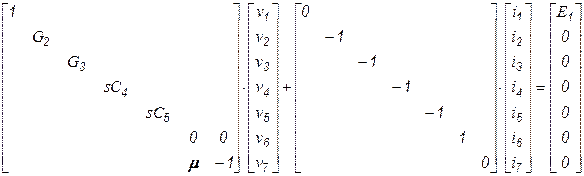Из примера видно, что коэффициенты табличной системы получаются чрезвычайно разряженными. Для сравнения различных методов удобно ввести показатель заполнения:

D = число ненулевых элементов/общее число элементов.

Для данного примера табличная система размерностью 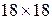имеет 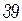ненулевых элементов. Следовательно, .

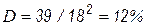Недостаток табличного метода заключается в большом размере систем уравнений и требовании специальных алгоритмов решения разряженных систем уравнений. Причем структура уравнений такова, что затрудняет использование более простых алгоритмов для разряженных матриц с симметричной структурой.