Модели распределенных структур

Различают однородные и неоднородные, одно- и многосвязанные, активные и пассивные распределенные структуры. Мы остановимся лишь на простейших однородных, односвязанных пассивных структурах.

Модели распределенных структур обычно описываются дифференциальными уравнениями в частных производных, называемых телеграфными. При периодическом воздействии уравнения в частных производных преобразуются в обыкновенные уравнения с постоянными коэффициентами. Обыкновенные дифференциальные уравнения с постоянными коэффициентами имеют аналитические решения, раскрывая которые с учетом граничных условий получают матрицу передачи конечного отрезка распределенной структуры. Определив матрицу передачи, легко перейти к любой другой системе параметров.

Матрицы передачи либо проводимости, полученные в результате решения дифференциальных уравнений, записываются через характеристические параметры распределенных структур.

Модель 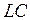-линии. Наиболее распространенной распределенной структурой являются 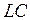-линии самого разнообразного вида. Это могут быть отрезки кабеля, симметричные и несимметричные полосковые линии и так далее. В случае распределенных структур корректно говорить лишь о модели бесконечно малого отрезка, выраженной через погонные параметры (т.е., параметры, отнесенные к единице длины). Так для 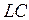- линии с потерями модель дифференциального участка приведена на рис. 5.29, а.

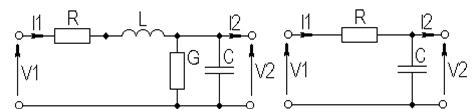
а) б)

Рисунок 5.29 – Дифференциальные модели линий передачи

Характеристические параметры 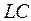-линии: волновое сопротивление 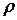и постоянная распространения 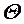определятся выражениями

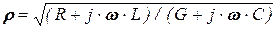, (5.84)

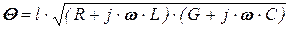, (5.85)

где 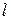- длина отрезка 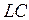-линии.

Модель 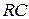-линии. Следующей распространенной простейшей распределенной структурой является 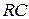-линия, представляющая собой частный случай 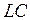-линии. 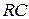-линии нашли применение в микроэлектронике при реализации активных фильтров. Модель дифференциального участка 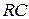- линии приведена на рис. 5.29, б.

Характеристические параметры 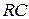-линии: характеристическое сопротивление 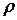и постоянная распространения 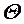определятся как

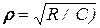, (5.86)

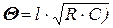, (5.87)

где 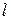– длина 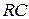-линии.

Структура матриц 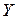-параметров отрезка 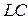-линии с потерями и 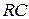- линии одинакова и может быть записана в виде

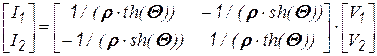, (5.88)

где 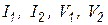- токи и напряжения на входе и выходе отрезка структуры; 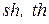– функции гиперболического синуса и тангенса комплексного аргумента.

Для 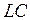-линии в случае отсутствия потерь характеристические параметры становятся вещественными и гиперболические функции вырождаются в тригонометрические функции.