Алгоритм Гаусса

МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ УРАВНЕНИЙ

Наиболее известным и эффективным из алгоритмов решения систем линейных уравнений общего вида является алгоритм Гаусса. В алгоритме Гаусса исходная линейная система уравнений

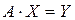(6.1)

решается в два этапа.

На первом этапе путем элементарных операций со строками и столбцами матрица 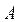приводится к треугольному виду. На втором этапе путем обратной подстановки находится вектор решения 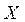. Чаще всего вектор решений 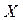формируется на месте вектора свободных членов .

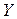Для удобства изложения ограничимся порядком системы уравнений 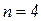, а вектор свободных членов 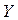присоединим к матрице коэффициентов 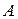, в качестве 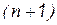-го столбца. В результате имеем следующую матрицу коэффициентов и свободных членов:

.

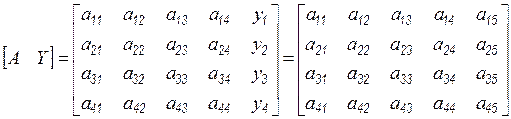На первом этапе для приведения матрицы коэффициентов к треугольному виду необходимо путем элементарных операций, столбец за столбцом, все коэффициенты ниже диагонали преобразовать в нули. В качестве первого шага для обнуления коэффициентов первого столбца ниже диагонали вычтем последовательно из второй строки первую, умноженную на 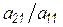; из третьей строки - первую, умноженную на 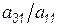; и, наконец, из последней – первую, умноженную на 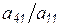. Покомпонентная запись этих операций имеет вид

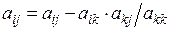, (6.2)

где 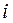– текущий номер строки 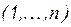; 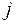- текущий номер столбца 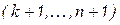; 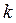– номер опорной строки (столбца) 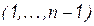. После первого шага система имеет вид

,

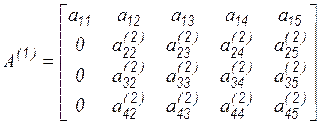где верхний индекс 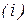означает номер шага.

На втором шаге за опорную считаем вторую строку, полученную после первого шага, и вычтем ее последовательно из третьей и четвертой строк, предварительно умножив соответственно на 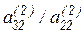и 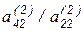, после чего получаем

.

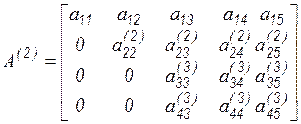Выполняя третий шаг, приходим к треугольному виду матрицы

.

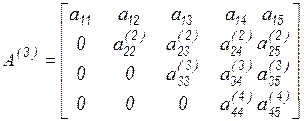На этом заканчивается первый этап и начинается второй – обратная подстановка.

Из последнего уравнения треугольной системы следует

,

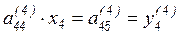в результате получаем

.

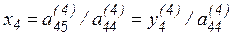Из предпоследнего уравнения треугольной системы имеем

,

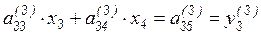или

,

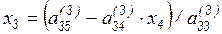и, подставив в него значение 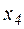, получим

.

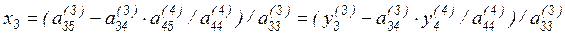Распространив далее подобные рассуждения, получим общее соотношение для произвольного шага обратной подстановки

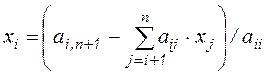, (6.3)

где, перебирая значения 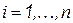, последовательно определим все компоненты вектора решений из рекуррентного выражения.

Рассмотрим обратную подстановку более подробно, чтобы полнее раскрыть ее содержание как набор базовых операций над строками.

Прежде всего, учитывая, что общее решение линейной системы уравнений (6.1) может быть представлено в виде

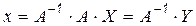, (6.4)

делаем вывод, что во время обратного хода исходная (треугольная) матрица должна быть приведена к единичной. Это означает, что элементы выше диагонали должны быть обнулены в результате элементарных операций над строками и строки должны быть нормированы относительно диагональных элементов. В соотношении (6.3) выражение в скобках как раз и соответствует операции над текущей строкой, а деление на 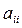– нормировке строки.

Так, в качестве первого шага обратной подстановки, для обнуления четвертого столбца над диагональю, необходимо из строк с третьей по первую, вычесть четвертую строку умноженную последовательно на

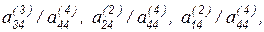
после чего нормировать четвертую строку относительно 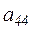. Для экономии операций целесообразно вначале нормировать текущую строку, а затем вычитать ее из других строк, предварительно умножив ее на соответствующий элемент строки текущего столбца.

В результате после первого шага обратной подстановки имеем

.

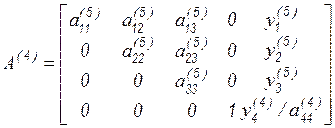На втором шаге нормируем третье уравнение и обнуляем третий столбец выше диагонали и т.д., пока не дойдем до первой строки и не нормируем ее.

В покомпонентной записи это соответствует операциям: а) нормировки для опорной строки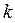

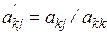, (6.5)

при 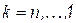; 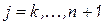, и б) обнуления элементов опорного столбца для строк, лежащих выше опорной

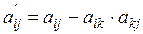, (6.6)

при ; ; .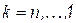

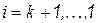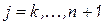Т.о., в результате прямого и обратного хода алгоритма Гаусса в (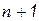)-ом столбце расширенной матрицы будет сформирован вектор решений .

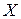Сделаем несколько важных замечаний по алгоритму Гаусса.

1. Прямой ход Гаусса совершается элементарными операциями над строками, как известно, не изменяющими значение ранга. В данном случае элементарные операции не изменяют и значение определителя, поэтому, перемножив диагональные элементы (до нормировки), после прямого хода получим значение определителя. Обычно на практике при решении линейной системы значение определителя получают как побочный продукт процедуры, предварительно заведя в ней соответствующую переменную с начальным значением единица и умножая эту переменную на каждом шаге прямого хода на диагональный элемент опорной строки.

2. Нормировка опорных элементов возможна и при прямом ходе, при этом перед нормировкой каждой строки значение опорного элемента умножается на текущее значение переменной определителя. В результате прямого хода получается верхняя треугольная матрица с единичной диагональю. Необходимость нормировки во время обратного хода в этом случае отпадает. Необходимо лишь скорректировать покомпонентные выражения, реализующие преобразования прямого и обратного хода.

3. Как отмечалось ранее (6.4), решение линейной системы в соответствии с алгоритмом Гаусса эквивалентно умножению исходной системы на обратную матрицу коэффициентов 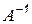. Отсюда следует простейший алгоритм получения обратной матрицы: если исходную матрицу расширить единичной матрицей, то в соответствии с выражениями

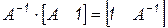
на месте единичной будет сформирована обратная матрица.

4. Алгоритм Гаусса легко интерпретировать как для нахождения вектора решения 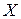, так и для обратной матрицы 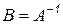, не прибегая к расширенной матрице в целях экономии памяти.

5. С целью уменьшения ошибки вычислений и исключения деления на нулевой диагональный элемент, обычно на каждом шаге прямого хода ищут максимальный по модулю элемент в оставшейся части матрицы (в оставшихся строках, либо столбцах) и путем перестановок строк и, если нужно столбцов, делают его диагональным. Произведенные перестановки учитываются в результирующем векторе решений и знаке определителя. Модификация алгоритма с полным либо частичным выбором главного значения требует большого числа операций, однако обладает повышенной точностью.

6. Соотношения (6.2) алгоритма Гаусса как его модификация используется для понижения порядка линейной системы уравнений путем исключения части переменных. При этом коэффициенты исходной системы преобразуются, оставляя ее инвариантной по отношению к оставшимся переменным.

Поясним суть исключения переменных на примере блочного представления системы

,

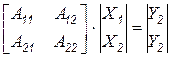где 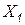– остающиеся переменные; 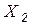– исключаемые переменные.

Записывая систему в виде

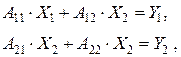
выражая 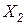из второго уравнения

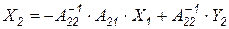
и подставляя в первое уравнение, получим укороченную эквивалентную систему уравнений понижения порядка линейной системы уравнений - блочную форму алгоритма Гаусса

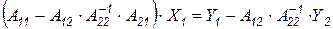. (6.7)

Это соотношение показывает, как трансформируется матрица коэффициентов и вектор свободных членов при понижении порядка системы.

Покомпонентная форма, соответствующая исключению по одной переменной, как следствие соотношения (6.7) имеет знакомый вид (см. (6.2)):

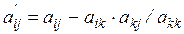, (6.8)

где 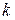– индекс исключаемой переменной (строки, столбца).

Для вектора свободных членов исключение 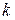-ой переменной соответствует выражению

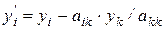, (6.9)

которое при желании можно трактовать как преобразование 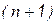-го столбца расширенной матрицы.

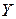В соответствии с (6.8), (6.9) на каждом этапе исключения преобразуют все элементы остающихся на данный момент строк и столбцов матрицы и компонент вектора . Приведенные соотношения соответствуют исключению одноименных компонент векторов 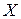и 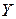, однако их можно трансформировать и на исключение разноименных компонент, что также имеет физическую интерпретацию.

7. Инверсию или обращение матрицы также можно интерпретировать через блочный алгоритм исключения. Так, рассматривая в качестве исходной систему

,

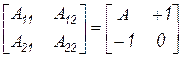и исключая по аналогии с (6.7) первую группу переменных на месте блока 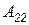, получим .

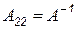Таким образом, один и тот же алгоритм или соотношения Гаусса применяются при решении линейных систем уравнений, исключении части переменных с целью сокращения размерности системы и при вычислении обратных матриц коэффициентов.