Алгоритм Гаусса-Жордана

Известно несколько модификаций алгоритма Гаусса. В частности, Жорданом была предложена модификация алгоритма, позволяющая решать систему уравнений за один проход.

Отличие заключается в том, что после выбора и нормировки опорной строки элементы опорного столбца обнуляются с помощью элементарных операций как под, так и над диагональю.

Для пояснения, ограничившись порядком 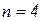, вновь обратимся к расширенной за счет вектора свободных членов матрице коэффициентов

.

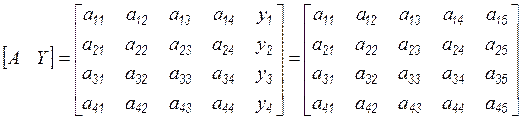Пусть первая строка является опорной, а диагональный элемент 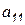– ведущим. Нормируем опорную строку относительно ведущего элемента и для обнуления первого столбца, за исключением ведущего элемента, вычтем из остальных строк первую – опорную, умноженную на элементы ведущего столбца соответствующих строк. В результате первого шага получим

.

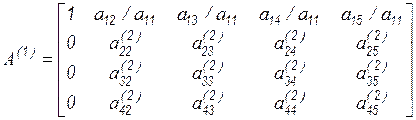На втором шаге нормируем вторую строку относительно 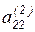и вычтем ее из остальных, предварительно умножая на соответствующий элемент ведущего столбца

.

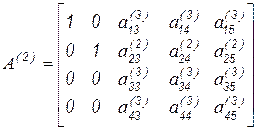Продолжая выбор ведущей строки до последней, на месте исходной матрицы получим единичную матрицу. На месте вектора свободных членов образуется вектор решений. Доказательство данного факта следует из эквивалентности решения системы действию на нее обратной матрицы

.

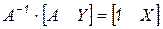Последовательность операций алгоритма Гаусса-Жордана может быть представлена в виде

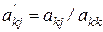, (6.10)

при ; ;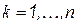

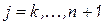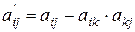, (6.11)

при 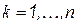; ; 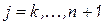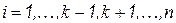, где 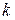– номер опорной строки.

Отметим некоторые особенности и модификации алгоритма Гаусса-Жордана:

1. Для повышения точности и надежности алгоритма также используют модификацию с полным либо частичным выбором главного значения.

2. Используя дополнительную переменную с единичным начальным значением и умножая ее перед нормировкой очередной строки на ведущий элемент, получим в результате значение определителя.

3. Известный метод оптимального исключения, позволяющий решать большие системы с малой оперативной памятью ЭВМ, является модификацией алгоритма Гаусса-Жордана, при котором вся матрица коэффициентов хранится во внешней памяти, а в оперативной памяти хранятся попарно опорная и текущая строки. В результате появляется возможность работать с системами уравнений, объем которых превышает оперативную память, но требуется многократный обмен с оперативной памятью, а значит, и время, кроме того, затрудняется выбор ведущего элемента.

4. Как и в алгоритме Гаусса, используя матрицу коэффициентов , расширенную единичной матрицей, в результате преобразований на месте единичной получим обратную матрицу.

5. Возможна модификация алгоритма для вычисления вектора решения 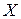и вычисления обратной матрицы 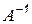без использования расширенной матрицы коэффициентов.

6. Интересна также модификация алгоритма Гаусса-Жордана для вычисления обратной матрицы на месте исходной:

а) среди оставшихся строк и столбцов ищем ведущий элемент и перестановкой строк и столбцов устанавливаем его на диагональ в опорной строке – вариант полного выбора главного значения;

b) заменяем ведущий элемент на обратный ;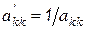

c) элементы ведущей строки умножаем на обратное значение ведущего элемента 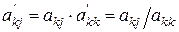, где ;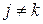

d) элементы на пересечении текущих строк и опорного столбца умножаем на 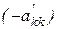, т.е. 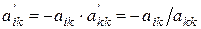, где ;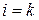

е) остальные элементы текущих строк преобразуются в соответствии с выражением 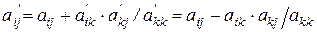, где 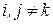, что соответствует вычитанию из текущих строк опорной, взвешенной на соответствующий элемент опорного столбца.

В алгоритме обращения матрицы на месте исходной важно строго соблюдать последовательность действий. Кроме перечисленной последовательности, возможна следующая: вначале можно выполнить пункт е), пропустив элементы текущей строки и столбца, затем пункт с), пропустив ведущей элемент, за ним пункт b) и, наконец, пункт d), заменяя деление умножением на обратное значение опорного элемента – другими словами, последовательность а); е); с); b); d). Приемлема также последовательность а); с); b); d); е).

Рассмотрим пример обращения матрицы на месте исходной для матрицы второго порядка по основной последовательности.

Изложение приведем в символьном виде, поэтому выбор главного значения будет отсутствовать. Пусть задана матрица

.

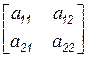Первый шаг алгоритма по основной последовательности. Выбираем в качестве опорной первую строку и ведущий элемент 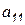. В результате нормировки ведущего элемента – пункт b) - имеем

.

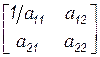Умножим элементы первой строки на обратное значение ведущего элемента – пункт с):

.

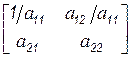Нормируем элементы опорного столбца – пункт d):

.

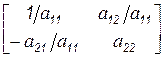Преобразуем элементы остальных строк и столбцов – пункт е):

.

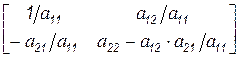Заметим, что элемент 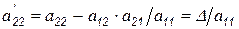, где 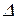- определитель матрицы второго порядка.

Второй шаг алгоритма: опорной является вторая строка, а ведущим элементом 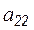. В результате нормировки ведущего элемента – пункт b) - имеем

.

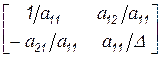Умножим элементы второй строки на обратное значение ведущего элемента – пункт с):

.

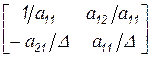Нормируем элементы опорного столбца – пункт d):

.

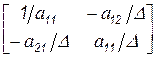Преобразуем элементы остающихся строк и столбцов – пункт е) - и, учитывая, что 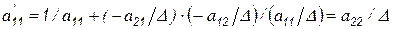, окончательно имеем

.

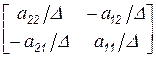Результат, как мы видим, полностью совпадает с обратной матрицей. Другое замечание, которое можно сделать, анализируя алгоритм, – это принципиальная важность выполнения пунктов с) и d) до либо после пункта е).

Таким образом, алгоритмы Гаусса и Гаусса-Жордана позволяют решать системы уравнений общего вида, находить обратные матрицы, понижать порядок уравнений и вычислять определители.