2014-02-12
4797
Схема Халецкого (LU-факторизация)
Одним из лучших методов решения систем линейных алгебраических уравнений общего вида является метод, основанный на разложении исходной матрицы на произведение треугольных, или метод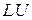 
-факторизации. Алгоритмы этого метода близки к алгоритмам метода Гаусса, хотя вычисления могут производиться в различной последовательности. Главным преимуществом метода 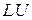-факторизации в сравнении с методом Гаусса является возможность более быстрого получения решений для различных векторов свободных членов, а также для транспонированной системы уравнений.
По числу операций, необходимых для решения конкретной системы, методы Гаусса и 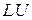-факторизации практически неразличимы. Однако из всех операций решения в методе 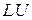-разложения почти половина приходится на этап факторизации и следующая половина - на собственно решение двух треугольных систем. В силу этого факта при необходимости решения системы, отличающейся лишь вектором свободных членов, получаем экономию на операциях разложения. Аналогично, когда необходимо решать транспонированную систему после исходной, можно воспользоваться предыдущей факторизацией и лишь сменить порядок решения треугольных систем в силу операции транспонирования.
|
|
|
В методе решения систем линейных уравнений, основанном на факторизации, предполагается, что исходная система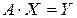 
(6.12)
может быть представлена в виде
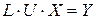, (6.13)
т.е.
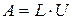. (6.14)
Причем для определенности полагается, что матрица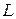 
является нижнетреугольной, а 
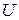– верхнетреугольной, причем с единичной диагональю.
Забегая несколько вперед, сразу отметим, что определитель треугольной матрицы равен произведению диагональных элементов, а определитель произведения матриц равен произведению их определителей. Откуда следует, что определитель матрицы 
равен произведению диагональных элементов нижнетреугольной матрицы :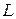
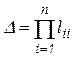. (6.15)
Ограничившись для наглядности порядком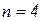 
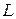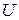, запишем - и -матрицы
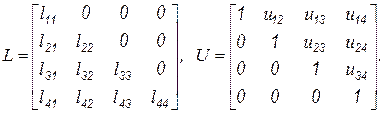
Схема Халецкого. Предполагая возможным разложение (6.14), вводя вспомогательный вектор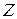 
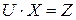(6.16)
и подставив данное выражение в уравнение (6.13), получим
-
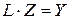(6.17)
две треугольные системы, эквивалентные исходной системе. Поскольку обе системы (6.16) и (6.17) треугольные, их решения достаточно тривиальны, причем в начале решаем систему (6.17) и находим вектор 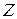, а затем из (6.16) окончательно находим 
.
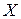Распишем подробнее алгоритм решения. Записывая систему (6.17) в виде
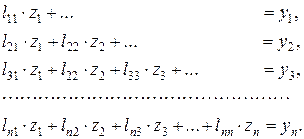
Для первых компонент вектора 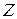можем записать
,
,
.
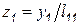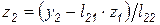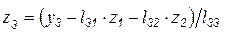Обобщая последовательность этих операций, называемых прямой подстановкой или прямым ходом, можем записать
; 
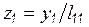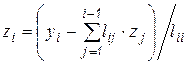, (6.18)
при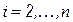 
.
Для того чтобы соотношение (6.18) имело смысл,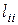 
не должны равняться нулю.
|
|
|
Теперь решим систему (6.16) в координатной форме:
,
,
,
,
.
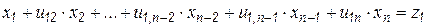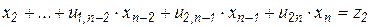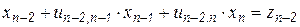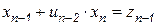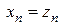Начиная с последней формулы, запишем выражения для нескольких компонент вектора решений :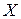
,
,
.
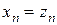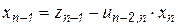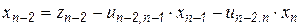Обобщая эту последовательность действий, называемую обратной подстановкой или обратным ходом, запишем
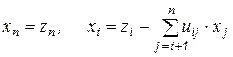, (6.19)
при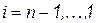 
.
Число операций, требуемых для выполнения как прямой, так и обратной подстановок, равно примерно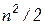 
, а в сумме для решения вместе с разложением требуется примерно 
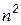операций.
Изучение соотношений (6.16) и (6.17) показывает, что компоненты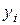 
используются только для определения 
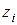и позднее не требуются. Аналогично 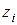не нужны после вычисления 
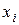. Следовательно, при такой системе расчетов векторы 
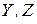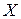и могут быть размещены в одних и тех же ячейках памяти ЭВМ. Коэффициенты треугольных систем – матрицы 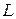и 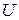, если не хранить единичную диагональ матрицы 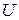, могут быть размещены на месте исходной матрицы коэффициентов . Следует также отметить эквивалентность обратных подстановок в схеме Халецкого и в методе Гаусса.
При изложении алгоритмов разложения для наглядности ограничимся порядком системы 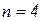, что не повлияет на общность рассуждений.
Суть алгоритма Краута. Предполагая, что разложение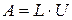 
существует, запишем произведение 
:
.
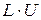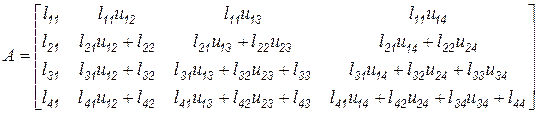Сравнивая компоненты этого произведения с компонентами матрицы , видим, что первый столбец произведения 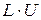равен первому столбцу матрицы , т.е. 
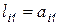, при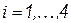 
. Первая строка произведения может быть использована для определения первой строки матрицы 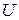. Действительно, т.к.
,
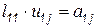при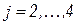 
, получаем
.
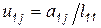Поскольку во втором столбце элементы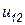 
и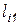 
известны, можем определить второй столбец матрицы :
,
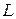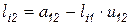где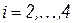 
. Теперь, т.к. известны 
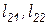и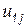 
, можно по второй строке произведения определить вторую строку матрицы :
,
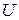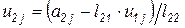при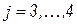 
. Далее, чередуя строки и столбцы, можно аналогичным образом найти остальные элементы матриц 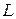и .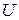
Чтобы получить общие соотношения, запишем произвольный элемент произведения :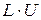
,
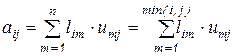где верхний предел суммы учитывает наличие нулевых элементов в матрицах 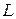и 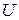. Рассмотрим произвольный элемент на или под главной диагональю матрицы , для которого 
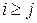, и заменим индекс 
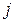на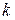 
. Учитывая при этом, что 
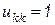, получим
,
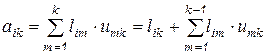откуда
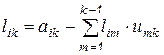, (6.20)
при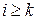 
и 
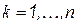. Аналогичным образом, рассматривая произвольный элемент над главной диагональю, для которого 
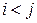, и используя 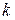вместо 
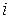, находим
,
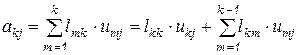откуда
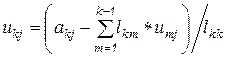, (6.21)
пр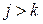и 
и .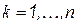
Эти соотношения для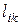 
и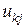 
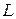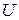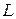есть алгоритм разложения на треугольные матрицы – алгоритм Краута. Заметим, что текущие элементы матриц и определяются текущим элементом матрицы и предыдущими элементами матриц и 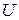. Отсюда, т.к. нулевые элементы и единичную диагональ матрицы 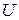запоминать не нужно, в процессе вычислений матрицы 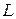и 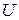могут быть записаны на месте матрицы , причем 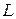расположена в нижнем треугольнике 
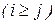, а 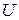– соответственно в верхнем треугольнике 
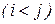матрицы .
Коротко алгоритм Краута как вариант чередования столбцов и строк можно представить следующей последовательностью действий:
1) положим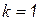 
и перейдем к пункту 3;
2) используя выражение (6.20), рассчитываем 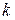-ый столбец матрицы 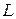и, если 
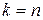, закончим процедуру разложения;
3) используя выражение (6.21), рассчитываем 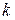-ую строку матрицы ;
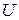4) положим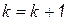 
и перейдем к пункту 2.
Кроме варианта чередования столбцов и строк, на основе соотношений (6.20) и (6.21) возможны варианты последовательного обхода по строкам либо по столбцам.
Если последовательно обходить (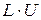)-произведение по строкам, то можно заметить, что, используя предыдущие соотношения (6.20) для 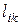при 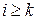и (6.21) для 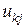при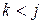 
, можно беспрепятственно определить все элементы матриц 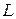и 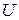. Аналогично можно организовать алгоритм вычисления элементов матриц 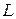и 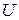, совершая обход по столбцам.
Преимущества этих вариантов алгоритма Краута проявляются при матрицах большого размера.
|
|
|
Известен также вариант алгоритма 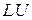-факторизации, основанный на приведении исходной матрицы к верхней треугольной форме по Гауссу [1], однако по сравнению с алгоритмом Краута он требует более частого обращения к матрице .
