Непрерывные СВ.
Случайной величиной (СВ) называют величину, которая в результате наблюдения (испытания) принимает то или иное значение, заранее не известное и зависящее от случайных обстоятельств.
Случайная величина.
Различают:
- дискретные СВ;
Дискретной называют такую СВ,которая принимает отдельные, изолированные (конечные или счетные) значения с определенными вероятностями.
Непрерывной называют такую СВ, которая может принимать любое значение из некоторого конечного или бесконечного числового промежутка (т.е. количество возможных значений непрерывной СВ бесконечно и несчетно).
Большинство СВ, рассматриваемых в экономике, имеет настолько большое число возможных значений, что их удобнее представлять в виде непрерывных СВ.
Наиболее полным, исчерпывающим описанием дискретной СВ является ее закон распределения. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Его можно задать таблично, аналитически (т.е. в виде формулы) и графически.
При табличном задании закона распределения дискретной СВ 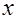 первая строка таблицы содержит ее возможные значения
первая строка таблицы содержит ее возможные значения 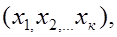 а вторая – их вероятности
а вторая – их вероятности 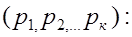
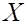 | 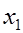 | 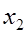 | … | 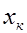 |
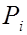 | 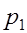 | 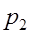 | … | 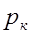 |
Обычно 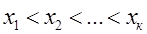 .
.
Такая таблица называется рядом распределения дискретной случайной величины.
Для любой дискретной случайной величины


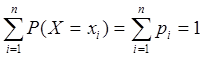 (14)
(14)
Если по оси абсцисс откладывать значения случайной величины, по оси ординат – соответствующие им вероятности, то можно получить (соединением точек) ломаную, называемую многоугольником или полигоном распределения вероятностей.
Аналитически СВ задается либо функцией распределения, либо плотностью вероятностей.
Функцией распределения СВ Х называют функцию 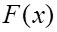 , определяющую вероятность того, что СВ Х принимает значение меньшее, чем
, определяющую вероятность того, что СВ Х принимает значение меньшее, чем 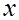 , т.е.
, т.е. 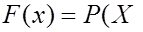 <
< 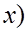 (15) Эту функцию также называют функцией накопленной вероятности или кумулятивной функцией распределения.
(15) Эту функцию также называют функцией накопленной вероятности или кумулятивной функцией распределения.
Из определения вытекают свойства функции распределения:
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: 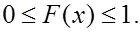 (16)
(16)
2.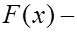 неубывающая функция,т.е.
неубывающая функция,т.е.
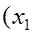 <
< 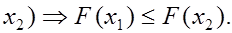 (17)
(17)
3. На минус бесконечности функция распределния равна нулю, на плюс бесконечности – равна единице: 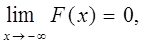
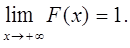 (18)
(18)
4. Вероятность попадания случайной величины Х в интервал 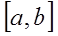 равна приращению ее функции распределения на этом интервале:
равна приращению ее функции распределения на этом интервале:
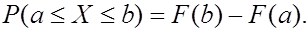 (19)
(19)
5. 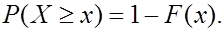 (20)
(20)
6. Если возможные значения СВ Х принадлежат отрезку 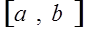 , то
, то
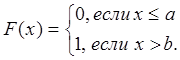 (21)
(21)
 2014-02-09
2014-02-09 2637
2637
