2014-02-09
1243
На первом этапе определяются средние значения признаков за весь период наблюдений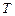 
для каждого объекта
,
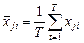где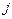 
– номер признака, 
;
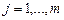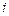– номер объекта, 
.
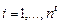На втором этапе строится пространственная модель связи (5.2) по вычисленным средним значениям признаков.
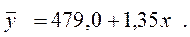
Данный метод приводит к удовлетворительным результатам только в том случае, если все объекты развиваются одинаково, т.е. имеют сходную динамику показателей.
B. Метод «заводо-лет»
Применяется в случае небольшого числа объектов, когда объем пространственной совокупности недостаточен для построения моделей связи показателей. Соответствующий алгоритм предусматривает увеличение объема выборки за счет того, что каждый объект включается в совокупность столько раз, сколько зафиксировано периодов наблюдения. Для расширенной выборки строится одна единственная пространственная модель (5.2).
Предположим, что n -объектов характеризуется одним факторным признаком (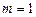
), наблюдались два периода времени (
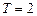). Расширенная совокупность включает 
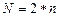наблюдений. Коэффициент регрессии линейного уравнения связи в этом случае равен
.
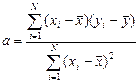Среднее по расширенной выборке значение результативного показателя
,
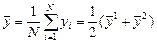где`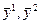
– средние значения результативного признака в первый и второй периоды соответственно.
Аналогично
.
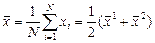Для отдельных периодов коэффициенты регрессии линейных уравнений связи в отдельный период равны
,
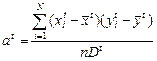где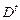 
– оценка дисперсии факторного признака в период t.
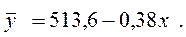
C. Метод усреднения показателей связи
На первом этапе строятся одногодичные уравнения связи (5.1). На втором этапе проводится непосредственное усреднение полученных параметров связи как
,
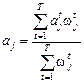где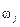 
– вес, в качестве которого можно использовать оценки дисперсии j - го фактора в период t –
.
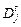5.2.2. Выбор вида пространственно - динамической
