Лаги Алмон представляют собой лаги, структуру которых можно описать с помощью полиномов, моделирующих наиболее общую их структуру.
Формально модель зависимости коэффициентов 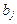 от величины лага
от величины лага 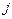 в форме полинома можно записать в следующем виде:
в форме полинома можно записать в следующем виде:
· для полинома 1-й степени: 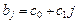 (рис.3 а));
(рис.3 а));
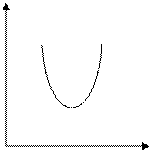
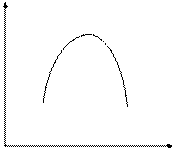
· для полинома 2-й степени: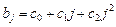 (рис.3 в), г), д));
(рис.3 в), г), д));
· для полинома 3-й степени: 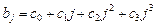 (рис.3 е)) и т.д.
(рис.3 е)) и т.д.

|
|
j j`
в) г)
bj bj
 |
 | |||
 | |||
j j
д) е)
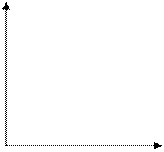
Рис.3 Графическое изображение структуры лага
Рассматривается полином произвольного k -го порядка, по отношению к которому все остальные структуры считаются частным случаем
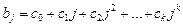 . (7.13)
. (7.13)
Каждый из коэффициентов модели с распределенным лагом (7.1) 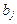 можно определить следующим образом:
можно определить следующим образом:
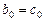 ;
;
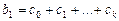 ;
;
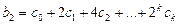 ;
;
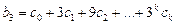 ;
;
……………………………….
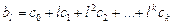 . (7.14)
. (7.14)
Подставив в (7.1) найденные соотношения для 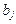 , получим
, получим
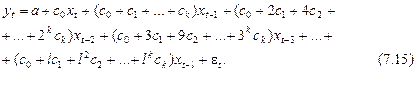
Перегруппируем слагаемые в (7.15) относительно 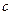 :
:
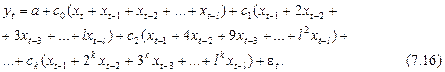
Обозначим слагаемые в скобках при 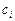 как новые переменные:
как новые переменные:
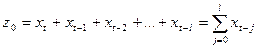 ;
;
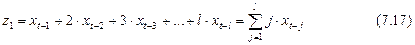
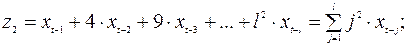
……………………………………………………..
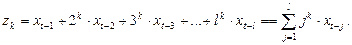
Перепишем модель (7.16) с учетом соотношений (7.17):
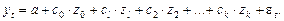 (7.18)
(7.18)
Основные этапы применения метода выглядят следующим образом.
· определение максимальной величины лага 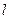 ;
;
· определение параметра 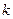 , определяющего структуру лага;
, определяющего структуру лага;
· расчет значений 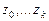 по соотношениям (7.17);
по соотношениям (7.17);
· определение параметров уравнения линейной регрессии (7.18);
· с помощью соотношений (7.14) рассчитываются параметры исходной модели с распределенным лагом.
Преимущества данного метода заключаются в том, что он является универсальным, т.е. может использоваться для моделирования процессов с различной структурой лага, а также в том, что при небольшом количестве переменных можно построить модель с распределенным лагом любой длины.
Применение метода Алмон связано с рядом проблем.
Во-первых, величина лага должна быть известна заранее. Рекомендуется брать максимально возможное значение. Выбор меньшего значения по сравнению с реальным может привести к неверной спецификации модели, т.е. не будет учтен фактор, оказывающий существенное влияние на результат. Воздействие этого фактора относится к остаткам модели, а это ведет к нарушению предпосылок МНК. Полученные оценки параметров будут неэффективными и смещенными. Выбор большей величины по сравнению с ее реальным значением приведет к включению в модель статистически незначимого фактора, что снизит эффективность оценок модели, но эти оценки все же будут несмещенными. Для обоснованного выбора величины лага рекомендуют рассчитать значения автокорреляционной функции различных порядков (п.4.4.5)
Во-вторых, необходимо определить рациональное значение 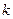 (степень полинома). Обычно на практике ограничиваются рассмотрением полиномов 2-го и 3-го порядков, применяя правило: выбранная степень полинома должна быть на единицу больше, чем число экстремумов в структуре лага. Если априорную информацию о структуре лага получить невозможно, то величину
(степень полинома). Обычно на практике ограничиваются рассмотрением полиномов 2-го и 3-го порядков, применяя правило: выбранная степень полинома должна быть на единицу больше, чем число экстремумов в структуре лага. Если априорную информацию о структуре лага получить невозможно, то величину 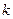 можно определить путем сравнения моделей, построенных для различных степеней
можно определить путем сравнения моделей, построенных для различных степеней 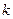 , и выбора наилучшей модели.
, и выбора наилучшей модели.
В-третьих, появится мультиколлинеарность 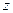 -факторов в том случае, если наблюдается сильная зависимость между исходными переменными. Но данная мультиколлинеарность меньше сказывается на оценке параметров
-факторов в том случае, если наблюдается сильная зависимость между исходными переменными. Но данная мультиколлинеарность меньше сказывается на оценке параметров 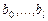 , чем если бы эти оценки были определены обычным МНК непосредственно к модели (7.1).
, чем если бы эти оценки были определены обычным МНК непосредственно к модели (7.1).
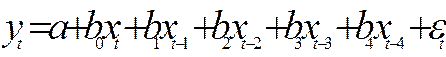
y- объем ВВП США (в % к уровню 1982 г.), млрд. долл.;
х – общая сумма расходов на приобретение новых заводов и оборудования в промышленности США (за 1959-1990 гг.), млрд.долл.
лаг
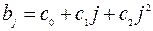
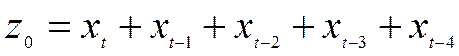
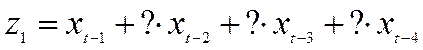
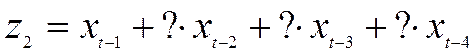
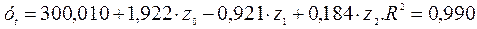 (66,200) (0,205) (0,299) (0,073)
(66,200) (0,205) (0,299) (0,073)

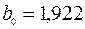
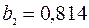
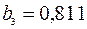
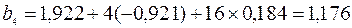
Модель с распределенным лагом:
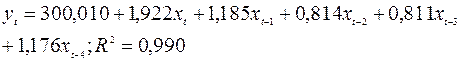 (66,200) (0,205) (0,100) ((),142) (0,096) (0,208)
(66,200) (0,205) (0,100) ((),142) (0,096) (0,208)
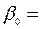
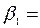
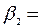
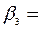
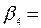
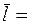
Результат применения обычного МНК
 2014-02-09
2014-02-09 1745
1745








