Оценка стоимости обыкновенной акции

Оценка стоимости привилегированных акций

Собственный капитал

Оценка стоимости облигационного займа.

Основными преимуществами облигационного займа как инструмента привлечения финансовых ресурсов являются:

возможность мобилизации значительных объемов денежных средств и финансирования крупномасштабных проектов на экономически выгодных для компании условиях без угрозы вмешательства инвесторов в управление его текущей финансово-хозяйственной деятельностью;

возможность маневрирования при определении характеристик выпуска: все параметры облигационного займа (объем эмиссии, процентная ставка, сроки, условия обращения и погашения и т.д.) определяются эмитентом самостоятельно;

возможность аккумулирования денежных средств частных инвесторов, привлечения финансовых ресурсов юридических лиц на достаточно длительный срок и на более выгодных условиях с учетом реальной экономической обстановки и состояния финансового рынка;

обеспечение оптимального сочетания уровня доходности для инвесторов, с одной стороны, и уровня затрат предприятия-эмитента на подготовку и обслуживание облигационного займа, с другой стороны;

Стоимость облигаций, выпущенных инвестором, приблизительно равна процентам, уплачиваемым по этим облигациям. Но при этом необходимо учитывать разницу между нарицательной стоимостью облигации и ценой ее реализации.

Полученная эмитентом при размещении облигационного займа сумма, как правило, ниже самого займа из-за расходов по выпуску займа.

Привилегированная акция подразумевает обязательство выплаты стабильного, фиксированного дивиденда, но не гарантирует возмещения своей номинальной стоимости.

Стоимость привилегированной акции = ожидаемый дивиденд / рыночная стоимость акции на момент оценки.

Обыкновенные акции, в отличие от привилегированных, не гарантируют своим владельцам выплаты дивидендов. Присущая обыкновенным акциям неопределенность усложняет определение цены акционерного капитала. Существует несколько подходов к решению данной задачи, из которых наиболее распространенные: модель Гордона (метод дисконтированных дивидендов, модель дивидендов с постоянным ростом и т.п.); модель оценки стоимости финансовых активов (CAPM); использование коэффициента «цена/прибыль» (P/E ratio). Выбор метода оценки зависит от имеющихся данных и степени их достоверности.

Основной моделью оценки обыкновенных акций является модель Гордона (или модель дивидендов постоянного роста). Ее можно применять для компаний, регулярно выплачивающих владельцам обыкновенных акций дивиденды.

Согласно данной модели, стоимость обыкновенных акций для предприятия рассчитывается по формуле:

Стоимость обыкновенной акции = (D1/P0) + g,

где D1 – дивиденд, ожидаемый в текущем году;

P0 – рыночная цена акции на момент оценки;

G – темп прироста дивидендов.

Пример. Рыночная цена акции в настоящий момент Р0 = 1000 руб. Ожидается, что дивиденд в текущем году будет равен D1 = 50 руб., а постоянный темп роста дивидендов g = 7%. Определим стоимость акционерного капитала.

Стоимость акционерного капитала = D1/ P0 + g = 50/1000 + 0,07 = 0,12=12%.

Если величину дивидендов трудно планировать заранее, можно использовать модель определения стоимости финансовых активов (CAPM – Capital Assets Pricing Model).

Преимущество этой модели заключается в простоте расчетов и легкости интерпретации их результатов. Однако для ее полноценного использования необходимо наличие зрелого финансового рынка с хорошо развитой информационной инфраструктурой.

Модель CAPM описывает зависимость между показателями доходности и риска финансового актива и рынка в целом.

Доходность ценной бумаги = Rf + β * (Rm - Rf);

Где Rf – безрисковая ставка дохода;

β – коэффициент бета (является мерой систематического риска);

Rm – общая доходность рынка в целом;

Коэффициент β выражается как ковариация (cov(Ri,Rm)) доходности актива Ri с доходностью всего рынка Rm по отношению к дисперсии доходности всего рынка d²(Rm), равный β = cov(Ri,Rm) / d²(Rm).

β-коэффициент для рынка в целом всегда равен единице.

Пример.

Определим значение коэффициента β для ценной бумаги. В таблице приведены данные о доходности ценной бумаги и всего рынка за девять периодов:

Период	Доходность акции (Ri,%)	Доходность рынка (Rm,%)
	-2	-4
	-1	-2
Средняя доходность	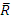4,8	6,7
β-коэффициент

Дисперсия доходности рынка:

d²(Rm) = ((5-6,7)² + (-4-6,7)² + (-2-6,7)² + (4-6,7)² + (9-6,7)² + (7-6,7)² + (12-6,7)² + (14-6,7)² + (15-6,7)²) / 9 = 39,6.

Коэффициент ковариации доходности акции и рынка:

Cov (Ri,Rm) = ((3-4,8)*(5-6,7)+(-2-4,8)*(-4-6,7)+(-1-4,8)*(-2-6,7)+(2-4,8)*(4-6,7)+(6-4,8)*(9-6,7)+(5-4,8)*(7-6,7)+(8-4,8)*(12-6,7)+(10-4,8)*(14-6,7)+(12-4,8)*(15-6,7))/9 = 27,9.

Коэффициент β = 27,9/39,6 = 0,70.

Полученный результат говорит о том, что если доходность рынка возрастет на 1%, то инвестор вправе ожидать роста доходности ценной бумаги в среднем на 0,7%.