РАВНОВЕСИЕ В ГЕТЕРОГЕННЫХ СИСТЕМАХ.
Предположим, что существует в состоянии термодинамического равновесия при 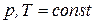 система, состоящая из
система, состоящая из 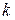 независимых компонентов и
независимых компонентов и 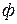 фаз. Общее условие термодинамического равновесия в системе в изобарно-изотермических условиях имеет следующий вид:
фаз. Общее условие термодинамического равновесия в системе в изобарно-изотермических условиях имеет следующий вид:
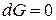 .
.
Вследствие аддитивности общая энергия Гиббса всей системы складывается из энергий Гиббса каждой из фаз:
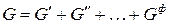 .
.
Продифференцируем:
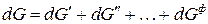 .
.
Для каждой из фаз в соответствии с уравнением (134)
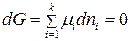 . (134)
. (134)
Подставив значение 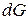 для каждой фазы, получим:
для каждой фазы, получим:
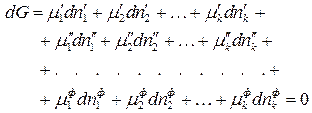 . (142)
. (142)
Уравнение (142) – выражает общее условие термодинамического равновесия в 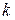 – компонентной,
– компонентной, 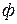 – фазной системе.
– фазной системе.
Решение такого уравнения затруднительно, но общее решение складывается из частных. Поэтому рассмотрим частный случай.
Пусть без нарушения равновесия из первой фазы во вторую перешло бесконечно малое число моль 1-го компонента 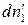 . При этом числа моль всех остальных компонентов постоянны во всех фазах и значения внешних параметров не изменяются:
. При этом числа моль всех остальных компонентов постоянны во всех фазах и значения внешних параметров не изменяются: 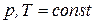 . Тогда условие равновесия (142) приобретает вид:
. Тогда условие равновесия (142) приобретает вид:
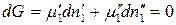 .
.
С учетом того, что 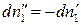 , получаем:
, получаем:
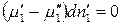 .
.
Произведение равно нулю, если хотя бы один из множителей равен нулю, но согласно условию 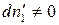 , тогда
, тогда
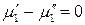 ;
;
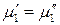 .
.
Следовательно, химический потенциал первого компонента одинаков в обеих фазах.
Рассматривая аналогичные частные случаи для других компонентов и фаз, получим, что при равновесии химический потенциал первого, второго и т.д.
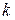 –го компонента также будет одинаков во всех фазах:
–го компонента также будет одинаков во всех фазах:
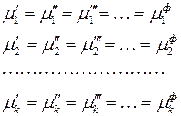 . (143)
. (143)
(143) – выражает условие термодинамического равновесия в 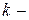 компонентной
компонентной 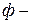 фазной системе и называется теоремой равновесия Гиббса.
фазной системе и называется теоремой равновесия Гиббса.
Формулировка теоремы Гиббса: условием термодинамического равновесия в гетерогенной системе является равенство химических потенциалов каждого компонента во всех фазах при постоянстве значений внешних параметров (т.е. при 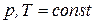 (чаще всего) или
(чаще всего) или 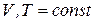 ).
).
 2014-02-12
2014-02-12 1386
1386