2. Проинтегрируем уравнение изобары (126) в неопределенных пределах (от абсолютного 0 до 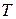 ) с учетом температурной зависимости
) с учетом температурной зависимости 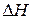 :
:
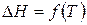
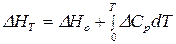 .
.
где 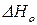 – тепловой эффект реакции при абсолютном нуле температур.
– тепловой эффект реакции при абсолютном нуле температур.
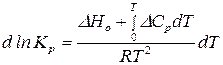 .
.
В результате получим:
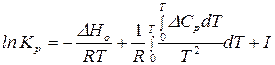 , (128)
, (128)
где 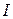 – константа интегрирования.
– константа интегрирования.
Для расчета константы равновесия необходимо определить численное значение 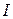 . Для конденсированных систем в области температур, прилегающих к абсолютному нулю, эта задача была решена на основе тепловой теоремы Нернста.
. Для конденсированных систем в области температур, прилегающих к абсолютному нулю, эта задача была решена на основе тепловой теоремы Нернста.
Конденсированными называют системы, не изменяющие своего агрегатного состояния при охлаждении до абсолютного нуля (кристаллические вещества).
С помощью III закона термодинамики можно показать, что для реакций, протекающих в конденсированных системах константа интегрирования 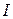 в уравнении (128) равна нулю. Тогда
в уравнении (128) равна нулю. Тогда
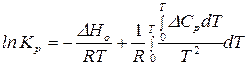 .
.
Для реакций, протекающих в идеальной газовой фазе 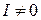 . На основе тепловой теоремы Нернста–Планка получено следующее уравнение для константы интегрирования:
. На основе тепловой теоремы Нернста–Планка получено следующее уравнение для константы интегрирования:
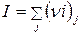 ,
,
где 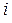 – химическая постоянная вещества;
– химическая постоянная вещества;
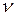 – стехиометрический коэффициент.
– стехиометрический коэффициент.
Суммирование проводится по всем газообразным веществам, принимающим участие в реакции.
Например: 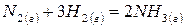 ;
;
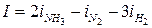 .
.
Тогда для газообразных систем уравнение для константы равновесия имеет вид:
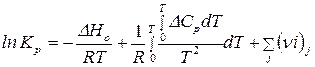 .
.
 2014-02-12
2014-02-12 521
521








