2014-02-12
590
УСЛОВИЕ ТЕРМОДИНАМИЧЕСКОГО РАВНОВЕСИЯ
ЛЕКЦИЯ 9
Для гомогенного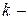 
компонентного раствора, находящегося в состоянии равновесия при постоянных значениях внешних параметров (
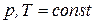), уравнение для изменения энергии Гиббса системы (88) примет вид:
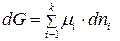(134)
или после интегрирования 
. (135)
Продифференцируем теперь уравнение (135) при условии, что переменными являются как масса, так и состав раствора. В этом случае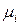 
тоже переменная величина, тогда
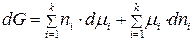. (136)
Сравним уравнения (134) и (136). Левые части уравнений одинаковы, поэтому, приравняв их, будем иметь:
.
Поделим левую и правую части последнего уравнения на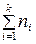 
, получим:
. (137)
(137) – у равнение Гиббса – Дюгема (впервые выведено Гиббсом и его учеником Дюгемом) выражает условие термодинамического равновесия в любом гомогенном растворе.
Запишем уравнение (137) для бинарной системы:
.
.
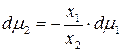Последнее уравнение устанавливает взаимосвязь между химическими потенциалами компонентов раствора.
Проинтегрируем уравнение в определенных пределах, получим:
.
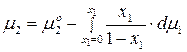где 
– химический потенциал второго компонента, когда в растворе отсутствует первый компонент (
).
С помощью данного уравнения можно рассчитать химический потенциал компонента, если известна зависимость от состава системы химического потенциала другого компонента.
Известно, что условием термодинамического равновесия в растворе при 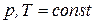, является минимум энергии Гиббса:
.
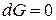Поскольку химический потенциал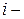 
го компонента раствора 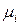представляет собой парциальную мольную энергию Гиббса 
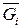, то уравнение Гиббса – Дюгема можно переписать:
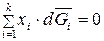. (138)
где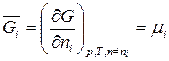 
.
Парциальная мольная энергия Гиббса, как и химический потенциал – интенсивное свойство раствора, т.е. зависит только от состава раствора и не зависит от его массы.
