СПЕЦИАЛЬНЫЕ ВИДЫ ВЕКТОРНЫХ ПОЛЕЙ
ЛЕКЦИЯ 9
Вклад гештальтизма в развитие психологии
Гештальтизм оставил заметный след в современной психологии и оказал влияние на отношения к проблемам перцепции, научения, мышления, изучения личности, мотивации поведения, а также на развитие социальной психологии. Недавние работы, являющиеся продолжением исследований гештальтистов, позволяют предположить, что их движение еще в состоянии внести вклад в развитие науки.
Гештальт-психология, в отличие от своего главного конкурирующего научного движения – бихевиоризма, многое сохранила от своей первоначальной оригинальности, благодаря чему ее основные принципы не растворились полностью в главном направлении психологической мысли. Гештальтизм продолжал поощрять интерес к сознательному опыту даже в те годы, когда в психологии доминировали идеи бихевиоризма.
Интерес гештальтистов к сознательному опыту был не таким, как у Вундта и Титченера, он строился на основе новейших феноменологических взглядов. Современные приверженцы гештальтизма убеждены, что опыт сознания по-прежнему должен изучаться. Однако, они признают, что он не может исследоваться с той же точностью и объективностью, как обычное поведение.
В настоящее время феноменологический подход в психологии шире распространен в Европе, чем в США, но его влияние на американскую психологию можно проследить на примере ее гуманистического движения. Многие аспекты современной когнитивной психологии обязаны своим происхождением работам Вертхеймера, Коффки и Келера и тому научному движению, которое они основали около 90 лет тому назад.
Оператор Гамильтона и его применения. Дифференциальные операции второго порядка. Потенциальные поля и их свойства. Соленоидальные поля и их свойства. Гармонические поля. Уравнение Лапласа. Свойства гармонических функций.
Все дифференциальные операции векторного анализа можно весьма значительно алгебраизировать при помощи оператора Гамильтона – символического вектора Ñ (читается – "набла"), определяемого равенством
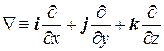 (8.1)
(8.1)
Сам по себе этот вектор смысла не имеет. Он приобретает смысл в сочетании со скалярной или векторной функцией, на которую он символически умножается в соответствии с правилами векторной алгебры.
1) Произведение Ñ на скалярную функцию u (x,y,z) дает градиент этой функции:
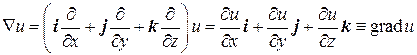 (8.2)
(8.2)
2) При помощи оператора Гамильтона, можно обобщить понятие производной по направлению. Вспомним, что для производной скалярного поля u по направлению единичного вектора b справедлива формула
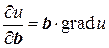 .
.
Введем скалярный дифференциальный символ:
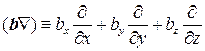 . (8.3)
. (8.3)
Тогда производную по направлению можно записать в виде
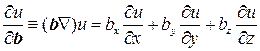 . (8.4)
. (8.4)
В такой записи, под b можно понимать любой вектор, не обязательно единичный.
3) По аналогии с понятием производной по направлению от скалярной функции, можно ввести понятие производной по направлению вектора b от векторной функции a:
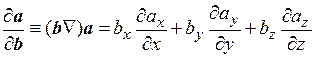 . (8.4)
. (8.4)
4) Скалярное произведение Ñ на векторную функцию a дает дивергенцию этой функции:
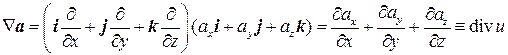 (8.5)
(8.5)
5) Векторное произведение Ñ на векторную функцию a дает ротор этой функции:
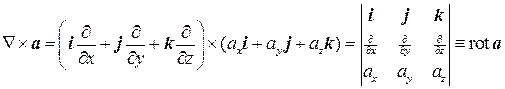 (8.6)
(8.6)
Таким образом, оператор Гамильтона и дифференциальные операции связаны следующим образом:
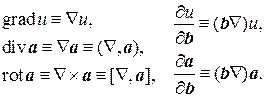
Пользуясь вектором Ñ, нужно помнить, что он является дифференциальным оператором, действующим на все функции, стоящие справа от него. Поэтому при преобразовании выражений, в которые входит Ñ, нужно учитывать не только правила векторной алгебры, но и правила дифференциального исчисления. Например, дифференциал произведения двух функций u и v равен
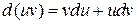 .
.
В соответствии с этим пишут
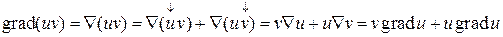 . (8.7)
. (8.7)
Здесь знаком "¯" отмечен тот множитель, к которому оператор Ñ должен применяться. Аналогично можно получить
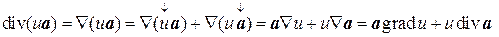 . (8.8)
. (8.8)
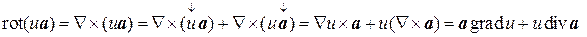 . (8.9)
. (8.9)
Целесообразность введения символического оператора Ñ состоит в том, что с его помощью удобно получать и записывать различные формулы векторного анализа. В частности,
 , (8.10)
, (8.10)
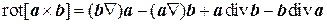 , (8.11)
, (8.11)
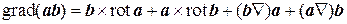 , (8.12)
, (8.12)
Замечание. Для вывода формулы (8.11) следует воспользоваться формулой двойного векторного произведения:
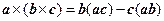 . (8.13)
. (8.13)
Для вывода формулы (8.12) следует предварительно найти Ñ(ac), где c =const. Поскольку c ´rot a = c ´(Ñ´ a)=Ñ(ac)–(c Ñ) a, то
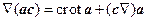 . (8.14)
. (8.14)
Тогда 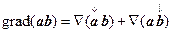 и, далее, следует воспользоваться формулой (8.14).
и, далее, следует воспользоваться формулой (8.14).
 2014-02-12
2014-02-12 2957
2957