В различных приложения векторного анализа часто встречаются так называемые дифференциальные операции 2-го порядка, т.е. попарные комбинации трех основных операций: градиента, дивергенции и ротора. Всего можно образовать 5 таких пар:
| 10. Ñ´(Ñj) º rot gradj º 0, | 30. Ñ(Ñ a) º div grad a, |
| 20. Ñ(Ñ´ a) º div rot a º 0, | 40. Ñ(Ñj) º div grad j, |
| 50. Ñ´(Ñ´ a) º rot rot a. |
Вообще говоря, комбинируя символы grad, div и rot, можно образовать 9 пар. Однако четыре из них: div div, grad grad, grad rot, rot div, не имеют смысла (объясните почему?).
Первое и второе выражения тождественно равны нулю. Это можно доказать, если расписать эти выражения по компонентам. Однако это легко объяснить, если привлечь аналогичные формулы из векторной алгебры. Для формулы 10 можно написать Ñ´(Ñj)=(Ñ´Ñ)j, но векторный квадрат, как известно, всегда равен нулю: a ´ a =0. Выражение 20 можно сравнить со смешанным произведением a (a ´ b)=0, т.к. a ^ a ´ b. То, что формулы 10 и 20 тождественно равны нулю, имеет особое значение для потенциальных и соленоидальных полей.
Остальные формулы не обязаны обращаться в нуль. Они часто встречаются в различных опросах механики и электродинамики, причем между ними существует взаимосвязь. Рассмотрим выражение 30, в котором первые два символа можно рассматривать как скалярный квадрат вектора Ñ:
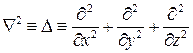 (8.15)
(8.15)
Этот дифференциальный оператор 2-го порядка называется оператором Лапласа (или лапласианом) и применим не только для скалярных, но и для векторных функций:
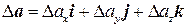 . (8.16)
. (8.16)
Далее, воспользовавшись формулой двойного векторного произведения (8.13), можно написать
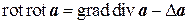 . (8.17)
. (8.17)
Пример 8.1. Вычислить Ñ2 a, Ñ(Ñ a), Ñ(Ñ´ a), Ñ´(Ñ´ a), если
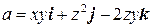 .
.
Решение. Находим дифференциальные операции 1-го порядка
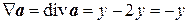 ,
,
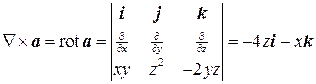 ,
,
а также лапласиан
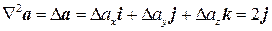 ,
,
где
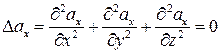 ,
,  ,
,
 .
.
После этого находим
 ,
,
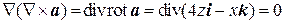 ,
,
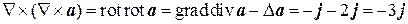 .
.
 2014-02-12
2014-02-12 1047
1047








