Полипоточные Системы Массового Обслуживания.
Предположим теперь, что в СМО с неограниченной очередью, о которой шла речь в Лекции 10, имеется не один, а несколько входных потоков (все они пуассоновские и каждый имеет свой параметр 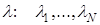 , так что всего потоков - N) и все потоки имеют экспоненциальное обслуживание, причем коэффициент
, так что всего потоков - N) и все потоки имеют экспоненциальное обслуживание, причем коэффициент 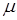 для
для 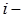 го потока есть число
го потока есть число 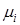 . Попадая в СМО, заявки становятся в очередь на обслуживание.
. Попадая в СМО, заявки становятся в очередь на обслуживание.
Можно доказать, что в такой ситуации суммарный входной поток в СМО тоже будет пуассоновским с параметром 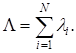
Можно также доказать, что функция распределения времени обслуживания равна:
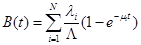 .
.
В теории массового обслуживания имеется следующий фундаментальный результат, называемой формулой Поллачека-Хинчина (в введенных обозначениях):
Среднее время ожидания в очереди в СМО описанного только что типа есть число
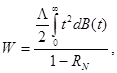
где 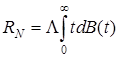 , причем предполагается, что выполнено условие:
, причем предполагается, что выполнено условие: 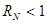 .
.
Неравенство 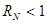 называется условием стационарности. Непосредственное интегрирование (по частям) показывает, что
называется условием стационарности. Непосредственное интегрирование (по частям) показывает, что
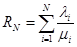 ;
;
полагают 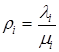 , так что
, так что 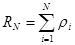 и
и 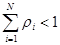 . Кроме того,
. Кроме того,
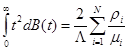 .
.
Полагают 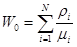 , так что формула Поллачека-Хинчина приобретает следующий краткий вид:
, так что формула Поллачека-Хинчина приобретает следующий краткий вид:
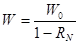 .
.
Легко заметить отсюда, что среднее число заявок i-го потока, ожидающих в очереди, есть величина
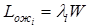 ;
;
суммарное число заявок из всех потоков, ожидающих в очереди, равно, следовательно,
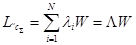 .
.
 2014-02-12
2014-02-12 546
546








