2014-02-12
681
Понятие игры двух лиц - антагонистической и с нулевой суммой. Схема классификации игр.
Игра - это сложный объект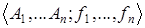 
, в котором 
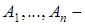множества и 
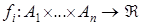- вещественно-значные функции, i=1,...,n. Элементы множества 
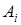называются стратегиями i-го игрока, а функция 
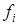- функцией выигрыша i-го игрока,
i=1,...,n. Каждый элемент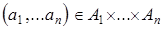 
называется реализацией игры, а число 
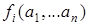- выигрышем i-го игрока, i=1,...,n в игре .
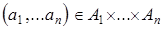Если n=2, то говорят об игре двух лиц. Если в игре двух лиц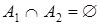 
, т.е. у игроков нет общих стратегий, то игра называется антагонистической. Если в антагонистической игре двух лиц множества стратегий конечны, то и игра называется конечной. Наконец, если сумма функций выигрыша 
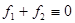, то конечная антагонистическая игра двух лиц называется игрой с нулевой суммой.
Именно такие игры (если не будет оговорок) мы будем рассматривать. Пусть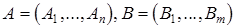 
- множества стратегий первого и второго игроков, соответственно. Положим 
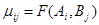, считая, что 
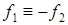и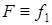 
и введем матрицу 
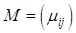, которая называется «платежной матрицей игры». Если положить 
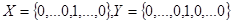, причем в первом векторе «1» стоит на месте № i, а во втором - на месте № j, то окажется выполненным равенство:
.
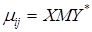Всякий числовой набор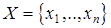 
, в котором все 
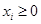и сумма 
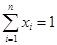, называется смешанной стратегией первого игрока; аналогично, смешанной стратегией второго игрока называется числовой набор 
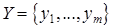, в котором все 
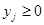и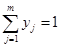 
.
Если в смешанной стратегии все координаты, кроме одной, равны нулю, то стратегия называется чистой. Всякая чистая стратегия естественным образом связана с определенной стратегией - ее номер, как элемента множества стратегий, совпадает с номером ненулевой координаты в чистой стратегии (кстати, эта ненулевая единственная координата равна, разумеется, единице).
