2014-02-12
583
Особенности пуассоновского потока заявок и экспоненциального времени об-служивания. СМО типа (m,n).
Из сказанного в предыдущей лекции следует, что в случае пуассоновского потока заявок имеется полное описание ряда случайной величины, которую представляет собой число заявок, поступивших за время t. Это позволяет подсчитать ее математическое ожидание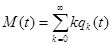 
. Соответствующий ответ выглядит так: 
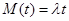. Это значит, что 
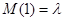. Следовательно, смысл пуассоновского параметра в том, что это - среднее число заявок, поступающих в единицу времени.
Можно провести аналогичные рассуждения в связи с экспоненциальным временем обслуживания. А именно, если
-
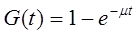функция распределения времени обслуживания (при неотрицательных значениях t, а при отрицательных - она равна нулю), то математическое ожидание времени обслуживания есть число
.
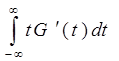Стандартное интегрирование по частям дает ответ - число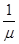 
. Следовательно, среднее время обслуживания одной заявки равно 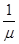(при экспоненциальном обслуживании); поэтому в единицу времени (при экспоненциальном обслуживании) в среднем обслуживается 
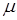заявок.
Рассмотрим теперь следующую модель СМО. Предположим, что ее узел обслуживания имеет n одинаковых устройств и очередная приходящая заявка попадает на любое из этих устройств для обслуживания. Если оказывается, что все устройства заняты, то заявка становится в очередь и ожидает, когда какое-либо устройство освободится. Предположим, что число мест в очереди равно m. Наконец, будем предполагать, что входной по-
ток заявок - пуассоновский с параметром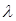 
, а время обслуживания - экспоненциальное с параметром 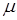. Такие СМО называются СМО типа (m, n).
Граф состояний такой СМО выглядит очень просто:
,
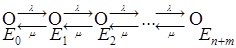причем около ребер-стрелок в данном случае указаны лишь интенсивности перехода из состояния в состояние.
