Как было сказано выше, важнейшая особенность СМО как объекта изучения состоит в том, что заявки приходят в СМО на обслуживание в случайные моменты времени. Следовательно, переход СМО из одного состояния в другое есть событие случайное. Пусть - вероятность того, что СМО переходит из состояния Ei в состояние Ej за период времени, причем здесь и всюду в дальнейшем, если только не будет оговорено иное, предполагается именно такая пара состояний (Ei, Ej), которая составляет ребро в графе состояний. Введенные вероятности называются переходными вероятностями СМО.
Если все переходные вероятности 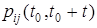 не зависят от аргумента
не зависят от аргумента 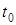 , т.е. для всех ребер графа состояний
, т.е. для всех ребер графа состояний 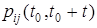 =
= 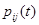 , то СМО называется стационарной. Всюду в дальнейшем именно такие и только такие СМО будут рассматриваться. Именно для стационарных СМО слова «граф состояний» обозначают не только тот граф состояний, который был введен выше, но еще и совокупность функций
, то СМО называется стационарной. Всюду в дальнейшем именно такие и только такие СМО будут рассматриваться. Именно для стационарных СМО слова «граф состояний» обозначают не только тот граф состояний, который был введен выше, но еще и совокупность функций 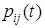 ; таким образом, граф состояний (стационарной) СМО - это взвешенный граф, в котором роль графа играет прежний граф состояний, а весовой функцией является функция, сопоставляющая каждому ребру функцию
; таким образом, граф состояний (стационарной) СМО - это взвешенный граф, в котором роль графа играет прежний граф состояний, а весовой функцией является функция, сопоставляющая каждому ребру функцию 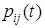 .
.
Функции 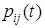 называются функциями переходных вероятностей или просто переходными вероятностями; бывает удобным в рассмотрениях следующий объект: матрица переходных вероятностей:
называются функциями переходных вероятностей или просто переходными вероятностями; бывает удобным в рассмотрениях следующий объект: матрица переходных вероятностей:
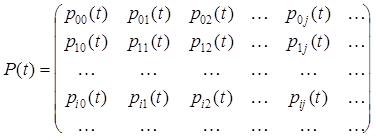 .
.
Заметим, что сумма элементов любого столбца этой матрицы (как и сумма элементов любой строки) равна единице – ведь эти элементы – вероятности событий, составляющих полную группу.
СМО называется системой без последействия, если функции 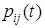 не зависят от того, как именно СМО попала в состояние Ei. Именно такие СМО рассматриваются в дальнейшем. Таким образом, мы будем обсуждать только стационарные СМО без последействия.
не зависят от того, как именно СМО попала в состояние Ei. Именно такие СМО рассматриваются в дальнейшем. Таким образом, мы будем обсуждать только стационарные СМО без последействия.
Основные характеристики СМО. Пуассоновский поток заявок, экспоненциальное время обслуживания.
Рассмотрим теперь величину 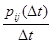 при
при 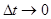 . Если эта величина стремится к нулю при
. Если эта величина стремится к нулю при 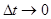 для всех i,j таких, что
для всех i,j таких, что 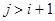 или
или 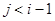 , то СМО называется ординарной. По смыслу это означает, что в ординарную СМО за короткий промежуток времени не может поступить более одной заявки и из ординарной СМО за короткий промежуток времени не может выйти более одной заявки.
, то СМО называется ординарной. По смыслу это означает, что в ординарную СМО за короткий промежуток времени не может поступить более одной заявки и из ординарной СМО за короткий промежуток времени не может выйти более одной заявки.
Мы будем в дальнейшем рассматривать только стационарные ординарные СМО без последействия.
Заметим следующее обстоятельство. Пусть 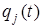 - вероятность того, что СМО попадает в течение времени t в состояние Ej и
- вероятность того, что СМО попадает в течение времени t в состояние Ej и 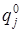 - вероятность того, что в некоторый начальный момент времени СМО была в состоянии Ej. Если обозначить
- вероятность того, что в некоторый начальный момент времени СМО была в состоянии Ej. Если обозначить 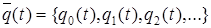 и
и 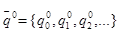 , то, согласно формуле полной вероятности и правилу умножения матриц, окажется выполненным равенство:
, то, согласно формуле полной вероятности и правилу умножения матриц, окажется выполненным равенство:
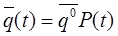 .
.
Промежуток времени между последовательно поступающими заявками в СМО есть величина случайная. Если функция распределения этой случайной величины имеет вид
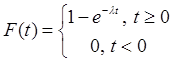
при некотором 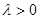 , то поток заявок называется пуассоновским.
, то поток заявок называется пуассоновским.
Время, в течение которого очередная заявка в СМО находится на обслуживании, также является величиной случайной. Если функция распределения этой случайной величины имеет вид
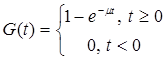
при некотором 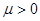 , то время обслуживания называется экспоненциальным.
, то время обслуживания называется экспоненциальным.
Прежде, чем анализировать особенности СМО с пуассоновским потоком заявок и экспоненциальным временем обслуживания, приведем некоторые стандартные конструкции.
Положим 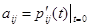 и введем матрицу
и введем матрицу 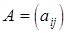 . Число
. Число 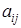 называется интенсивностью перехода СМО из состояния
называется интенсивностью перехода СМО из состояния 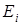 в состояние
в состояние 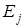 . Когда
. Когда 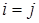 , число (
, число (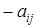 ) называют интенсивностью выхода СМО из состояния
) называют интенсивностью выхода СМО из состояния 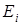 . Полезно заметить, учитывая, что при
. Полезно заметить, учитывая, что при 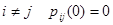 , а при
, а при 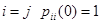 , справедливы неравенства:
, справедливы неравенства:
при 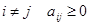 , а при
, а при 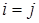
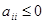 .
.
Матрица 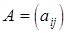 называется матрицей интенсивностей СМО.
называется матрицей интенсивностей СМО.
Можно доказать, что вероятности 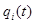 , введенные в этой лекции, удовлетворяют системе линейных дифференциальных уравнений
, введенные в этой лекции, удовлетворяют системе линейных дифференциальных уравнений
(7.1) 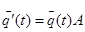
при начальных условиях 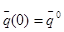 (здесь
(здесь 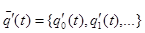 ).
).
Из ординарности СМО следует, что в ее матрице интенсивностей отличными от нуля могут быть элементы только на главной диагонали и на двух ближайших к ней и параллельных ей линиях:
 .
.
Это обстоятельство делает систему уравнений (7.1) более конкретной. В частном случае, например, при пуассоновском потоке входных заявок (можно проверить, что в этом случае СМО будет стационарной, ординарной и без последействия) и полном отсутствии обслуживания (это значит, что заявки только поступают в СМО, но не покидают СМО) матрица A принимает вид
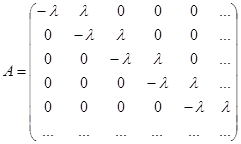 ,
,
после чего система (7.1) решается рекуррентно стандартными средствами. В результате получается ответ:
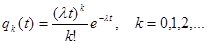 .
.
Это означает, что в СМО с пуассоновским потоком заявок и любым режимом обслуживания вероятность поступления k заявок
за время t равна 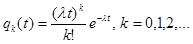 .
.
 2014-02-12
2014-02-12 619
619








