Характеристики СМО типа (m,n).
Основной характеристикой СМО типа (m, n) являются вероятности 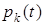 того, что в момент времени t СМО находится в состоянии
того, что в момент времени t СМО находится в состоянии 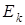 . Для функций
. Для функций 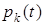 можно построить систему дифференциальных уравнений, допускающую явное решение. В основе соответствующих построений лежат два обстоятельства, на которые мы укажем, но сами построения оставим за пределами данного курса лекций.
можно построить систему дифференциальных уравнений, допускающую явное решение. В основе соответствующих построений лежат два обстоятельства, на которые мы укажем, но сами построения оставим за пределами данного курса лекций.
Первое обстоятельство. Положим 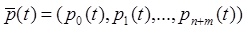 ; тогда, в соответствии с правилом умножения матриц и формулой полной вероятности, окажется выполненным равенство
; тогда, в соответствии с правилом умножения матриц и формулой полной вероятности, окажется выполненным равенство
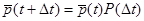 ,
,
где, как и было ранее, символ P обозначает матрицу переходных вероятностей.
Второе обстоятельство. Матрицу 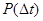 можно подробно описать в процессе, когда
можно подробно описать в процессе, когда 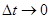 . Если в этом описании обозначать через
. Если в этом описании обозначать через 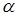 любую бесконечно малую при
любую бесконечно малую при 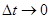 , то вот результат соответствующего описания:
, то вот результат соответствующего описания:
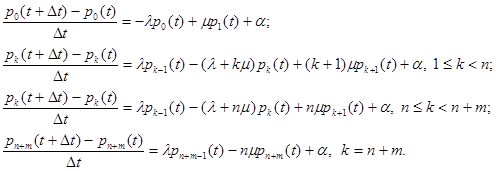
Если теперь перейти в этих соотношениях к пределу при 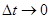 , то получатся дифференциальные уравнения относительно искомых функций
, то получатся дифференциальные уравнения относительно искомых функций 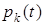 ; вот вид соответствующей системы уравнений:
; вот вид соответствующей системы уравнений:
(9.1) 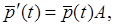
где A - матрица из констант.
Сформулируем теперь знаменитую теорему о финальных вероятностях, на которой основаны дальнейшие сведения о СМО типа (m, n):
Все функции 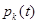 имеют предел при
имеют предел при 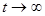 . Все производные
. Все производные 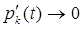 при
при 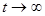 .
.
Положим 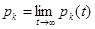 ; числа
; числа 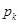 называются финальными или стационарными вероятностями.
называются финальными или стационарными вероятностями.
Если в (9.1) перейти к пределу при 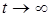 , то, с учетом теоремы о финальных вероятностях, получим систему линейных алгебраических уравнений относительно финальных вероятностей:
, то, с учетом теоремы о финальных вероятностях, получим систему линейных алгебраических уравнений относительно финальных вероятностей:
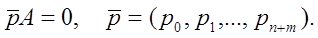
С учетом всего сказанного выше эту последнюю алгебраическую систему можно записать явно и, так же в явном виде, - решить. Отметим, что при этом решении надо будет воспользоваться тем, что по смыслу 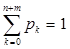 . Приведем лишь результат решения, обозначив для удобства через
. Приведем лишь результат решения, обозначив для удобства через 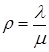 :
:
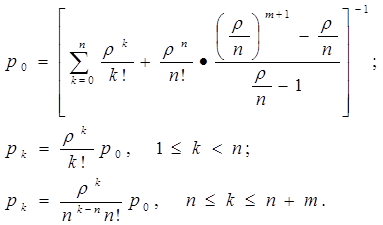
Приведем теперь основные характеристики рассматриваемых СМО.
Вероятность того, что в СМО занято обслуживанием ровно k устройств равна 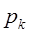 ,
, 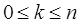 .
.
Вероятность отказа заявке есть число 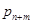 .
.
Число занятых устройств в СМО есть, очевидно, величина случайная. Ее математическое ожидание - это среднее число занятых устройств. Оно может быть вычислено и вот результат:
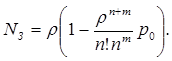
Если 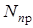 - среднее число простаивающих устройств, то, очевидно,
- среднее число простаивающих устройств, то, очевидно,
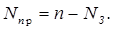
Часто используются коэффициенты простоя 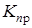 и занятости
и занятости 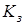 (эти формулы и представляют собой определения):
(эти формулы и представляют собой определения):
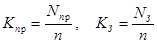 .
.
Относительная пропускная способность СМО - это дробь 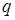 , в числителе которой указывается количество обслуженных заявок, а в знаменателе - общее число заявок, поступавших в СМО. Можно заметить, что
, в числителе которой указывается количество обслуженных заявок, а в знаменателе - общее число заявок, поступавших в СМО. Можно заметить, что
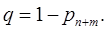
Абсолютная пропускная способность A - это среднее число заявок, обслуживаемых в единицу времени:
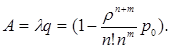
Среднее число заявок, ожидающих в очереди - величина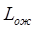 - может быть вычислено как соответствующее математическое ожидание; вот результат:
- может быть вычислено как соответствующее математическое ожидание; вот результат:

Среднее число заявок, поступающих в СМО, - это число
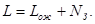
Среднее время W ожидания заявки в очереди также представляет собой величину, которую рассчитывают как математическое ожидание. Соответствующий результат оказывается таким:
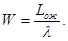
И, наконец, последняя характеристика: среднее время пребывания заявки в СМО - число V:
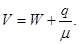
Лекция 10
Эрланговские СМО и СМО с неограниченной очередью, их основные характеристики.
СМО без ожидания или эрланговские СМО - это такие СМО, в которых нет места для очереди; если узел обслуживания занят в момент прихода очередной заявки, то заявка теряется. Предполагается, что в эрланговских СМО входной поток заявок обязательно пуассоновский, а время обслуживания - экспоненциальное.
Легко заметить, что эрланговские СМО - это СМО типа (m,n) при 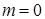 . Поэтому все рассуждения о СМО типа (m,n) можно адаптировать к этому частному случаю. В этом числе, формулы Эрланга - формулы, выражающие вероятности
. Поэтому все рассуждения о СМО типа (m,n) можно адаптировать к этому частному случаю. В этом числе, формулы Эрланга - формулы, выражающие вероятности 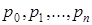 - можно
- можно
получить из формул для финальных вероятностей СМО типа (m,n) при 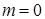 . Вот результат (по-прежнему
. Вот результат (по-прежнему 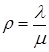 ):
):
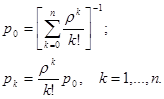
В частности, вероятность отказа равна 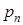 , среднее число занятых устройств равно
, среднее число занятых устройств равно 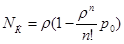 , относительная пропускная способность
, относительная пропускная способность 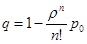 , абсолютная пропускная способность
, абсолютная пропускная способность 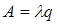 .
.
Рассмотрим второй «крайний» случай СМО типа (m,n), когда 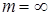 . Это означает, что очередь может быть как угодно большой. Вероятности
. Это означает, что очередь может быть как угодно большой. Вероятности 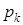 имеют здесь смысл при любом целом неотрицательном k. Выражение для
имеют здесь смысл при любом целом неотрицательном k. Выражение для 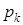 можно получить предельным переходом при
можно получить предельным переходом при 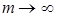 из выражения для
из выражения для 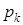 в случае (m,n). Если
в случае (m,n). Если 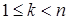 , то все требования находятся на обслуживании, а очередь пуста; соответствующая вероятность:
, то все требования находятся на обслуживании, а очередь пуста; соответствующая вероятность:
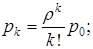
при 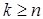 на обслуживании находятся n заявок и k-n находятся в очереди; соответствующая вероятность:
на обслуживании находятся n заявок и k-n находятся в очереди; соответствующая вероятность:
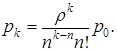
Для вычисления 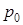 воспользуемся тем фактом, что, как и положено вероятностям полной группы событий,
воспользуемся тем фактом, что, как и положено вероятностям полной группы событий, 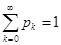 . Отсюда -
. Отсюда -
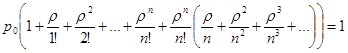 ;
;
вероятность 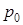 будет отлична от нуля только при одном условии: геометрическая прогрессия, стоящая в скобках в последнем соотношении, сходится. Это возможно только при условии
будет отлична от нуля только при одном условии: геометрическая прогрессия, стоящая в скобках в последнем соотношении, сходится. Это возможно только при условии
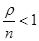 .
.
Это неравенство называется условием стационарности СМО с ожиданием (не путать с общим понятием стационарности СМО!). Если 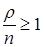 , то это означает, что СМО не справляется с обслуживанием и очередь всё
, то это означает, что СМО не справляется с обслуживанием и очередь всё
возрастает.
Если же условие стационарности 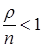 выполнено, то
выполнено, то
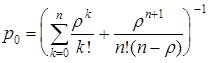 .
.
По смыслу легко заметить, что в рассматриваемых СМО вероятность отказа равна 0, относительная пропускная способность равна 1, абсолютная пропускная способность равна 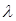 .
.
Среднее число занятых устройств:
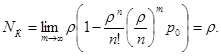
Среднее число простаивающих устройств:
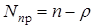 .
.
Параметр 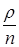 называется уровнем загрузки СМО.
называется уровнем загрузки СМО.
Среднее число требований, ожидающих в очереди в обсуждаемых СМО:
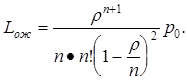
Среднее число заявок, находящихся в СМО:
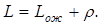
Среднее время ожидания заявки в очереди:
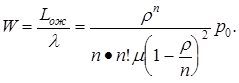
И, наконец, среднее время пребывания заявки в СМО:
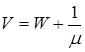 .
.
 2014-02-12
2014-02-12 903
903








