Определение: Направленный отрезок 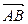 называется вектором, А- начало вектора, В- конец.
называется вектором, А- начало вектора, В- конец.
Определение: Вектор у которого начало и конец совпадает, называется нулевым
Длина вектора обозначается: 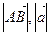
Определение: Если 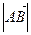 =1, то вектор
=1, то вектор 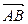 называется единичным.
называется единичным.
Определение: Вектора 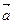 и
и 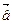 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Определение: Вектора 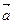 и
и 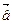 называются равными, если они коллинеарные, одинаково направленные и их длины равны.
называются равными, если они коллинеарные, одинаково направленные и их длины равны.
Проекции x, y, z вектора 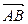 на оси координат называют координатами
на оси координат называют координатами 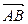 (x, y, z)
(x, y, z)
Если А(x1, y1, z1) и В(x2, y2, z2), то 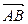 (x2-x1; y2-y1; z2-z1)
(x2-x1; y2-y1; z2-z1)
Если 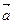 (x, y, z), то
(x, y, z), то 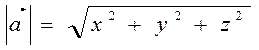
Обозначим через α, β, γ – углы между 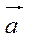 и осями координат, получим:
и осями координат, получим:
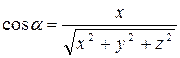
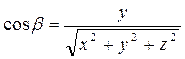
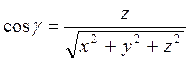
cos α, cos β, cos γ – называют направляющими косинусами вектора 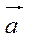
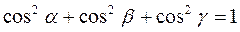
Определение Линейными операциями над векторами называются операции сложения и вычитания векторов, умножение вектора на число.
Определение Суммой векторов 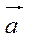 и
и 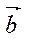 называется вектор
называется вектор 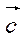 , который идет из начала вектора
, который идет из начала вектора 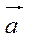 в конец вектора
в конец вектора 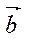 , при условии, что вектор
, при условии, что вектор 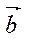 приложен к концу вектора
приложен к концу вектора 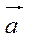
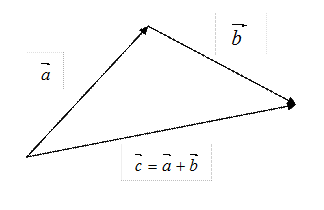
Правило треугольника
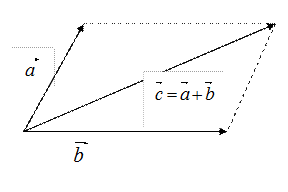
Правило параллелограмма
Определение Разностью векторов 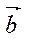 -
- 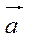 называется вектор, который в сумме с векторам
называется вектор, который в сумме с векторам 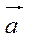 дает вектор
дает вектор 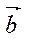
Определение Произведением λ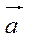 называется вектор, который коллинеарен
называется вектор, который коллинеарен 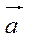 и имеет длину равную
и имеет длину равную 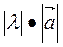 и направление такое же как вектор
и направление такое же как вектор 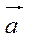 , если λ>0 и противоположное если λ<0
, если λ>0 и противоположное если λ<0
Т1 Если 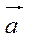 (x1, y1, z1)
(x1, y1, z1) 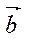 (x2, y2, z2), то
(x2, y2, z2), то 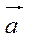 +
+ 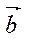 (x1+x2, y1+y2, z1+z2)
(x1+x2, y1+y2, z1+z2)
Т2 Если 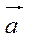 (x, y, z), то λ
(x, y, z), то λ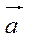 (λx, λy, λz)
(λx, λy, λz)
Признак коллинеарности векторов.
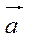 (x1, y1, z1)
(x1, y1, z1) 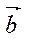 (x2, y2, z2), то
(x2, y2, z2), то 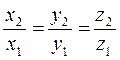
Пусть 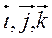 - единичные векторы
- единичные векторы 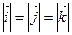 =1, каждый из них направлен на оси в положительную сторону, то
=1, каждый из них направлен на оси в положительную сторону, то 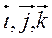 - базис
- базис
Любой вектор 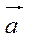 может быть разложен по базису
может быть разложен по базису 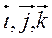 , т.е.
, т.е. 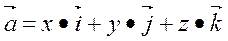
 2014-02-12
2014-02-12 4794
4794








