2014-02-12
2191
Определение Скалярным произведением двух не нулевых векторов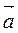 
и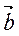 
называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними.
Обозначается ·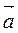
·= 
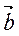
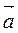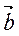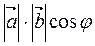
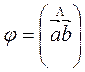
Свойства скалярного произведения.
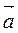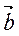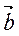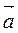- ·=·(свойство перестановочности сомножителей)
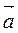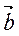- (l)·=l(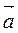·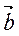) (свойство сочетательности)
- · (+
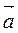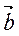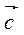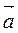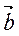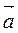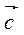)=·+·(свойство распределительности)
- ·=
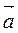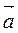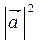
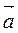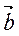- ·=0, если 
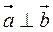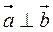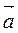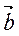и обратно, если ·=0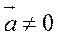 
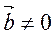
Выражение скалярного произведения через координаты векторов.
Т1 Если векторы 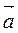и 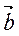заданы своими координатами 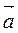(x1, y1, z1) 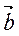(x2, y2, z2), то их скалярное произведение определяется формулой:
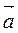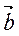·=x1x2+y1y2+z1z2
Следствие 1 Необходимым и достаточным условием перпендикулярности векторов 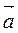(x1, y1, z1) и 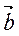(x2, y2, z2) является равенство x1x2+y1y2+z1z2=0
Следствие 2 Угол между векторами 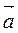(x1, y1, z1) и 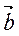(x2, y2, z2) определяется равенством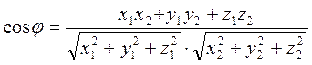 
Например Найти угол между векторами 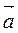(1, 1, 0) и 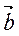(1, 0, 1)
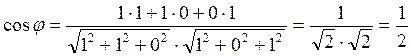j=600
Ответ: j=600
