Определение Матрицей – называется таблица чисел содержащая определенное количество строк и столбцов
Элементами матрицы являются числа вида aij, где i- номер строки j- номер столбца
Пример 1 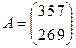 i = 2 j = 3
i = 2 j = 3
Обозначение: А= 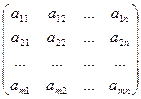
Виды матриц:
1. Если число строк не равно числу столбцов 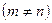 , то матрица называется пря моугольной:
, то матрица называется пря моугольной:
Пример 2 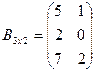
2. Если число строк равно числу столбцов 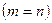 , то матрица называется квадратной:
, то матрица называется квадратной:
Пример 3 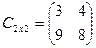
Число строк или столбцов квадратной матрицы называется ее порядком. В примере n = 2
Рассмотрим квадратную матрицу порядка n:
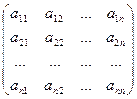
Диагональ, содержащая элементы a11, a22 ……., ann, называется главной, а диагональ, содержащая элементы а12, а2n-1, …….an1 – вспомогательная.
Матрица, у которой отличны от нуля только элементы, находящиеся на главной диагонали, называется диагональной:
Пример 4 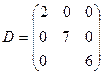 n = 3
n = 3
3. Если у диагональной матрицы элементы равны 1, то матрица называется единичной и обозначается буквой Е:
Пример 6 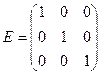 n = 3
n = 3
4. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается буквой О
Пример 7 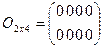
5. Треугольной матрицей n-ого порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:
Пример 8 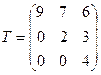 n = 3
n = 3
Действия над матрицами:
Суммой матрицы А и В называется такая матрица С, элементы которой равны сумме соответствующих элементов матриц А и В.
Пример 9 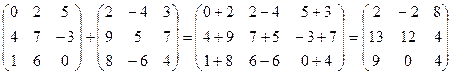
Складывать можно только матрицы, имеющие одинаковые число строк и столбцов.
Произведением матрицы А на число k называется такая матрица kA, каждый элемент которой равен kaij
Пример10 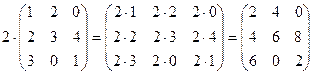
Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.
Произведение матриц. Что бы умножить матрицу на матрицу, необходимо выбрать первую строку первой матрицы и умножить на соответствующие элементы первого столбца второй матрицы, результат сложить. Этот результат расположить в результатирующей матрице в 1-ой строке и 10ом столбце. Аналогично выполняем действия со всеми остальными элементами: 1-ую строку на второй столбец, на 3-ий и т.д., затем со следующими строками.
Пример 11 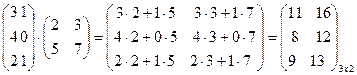
Умножение матрицы А на матрицу В возможно только в том случае, если число столбцов первой матрицы равно числу строе второй матрицы.
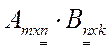 - произведение существует;
- произведение существует;
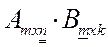 - произведение не существует
- произведение не существует
Примеры 12 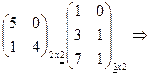 последнюю строчку во II матрицы умножать не с чем, т.е. произведение не существует
последнюю строчку во II матрицы умножать не с чем, т.е. произведение не существует
Транспонирование матрицы называется операция замены элементов строки на элементы столбца:
Пример13 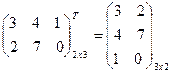
Возведением в степень называется последовательное перемножение матрицы саму на себя:
Пример 14 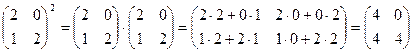
Возводить в степень можно только квадратные матрицы.
Определение Матрица А-1 называется обратной к матрице А, если выполняется условие А-1*А=1
Свойство матрицы
1. Переместительный закон относительно сложения
А+В = В+А – выполняется
Пример 15 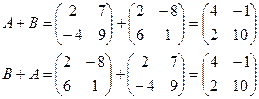
2. Распределительный закон 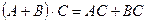 - выполняется:
- выполняется:
Пример 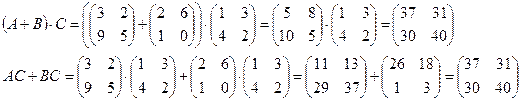
3. Переместительный закон относительно умножения 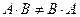 - не выполняется
- не выполняется
Пример 17 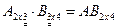
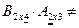 произведение не существует
произведение не существует
Пример 18 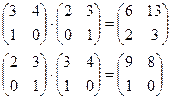
 2014-02-12
2014-02-12 47178
47178








