Объем цилиндрического тела

Приложения двойного интеграла

Как уже показано (п.1.2) объем цилиндрического тела находится по формуле

V = ,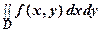

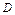
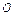
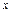
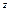
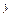
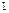
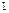
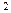
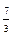где z = f (x, y) – уравнение поверхности, ограничивающей тело сверху, основание тела –

область D.

Пример 1. Найти объем тела, ограниченного поверхностями x ² + y ² – z + 1 = 0 и

x ² + y ² + 3 z – 7 = 0 (рис.1).

Данное тело ограничено двумя параболоидами. Решая систему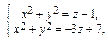

находим линию их пересечения x ² + y ² = 1, z = 2. Искомый объем равен разности

объемов двух цилиндрических тел с одним основанием (круг x ² + y ² ≤ 1) и ограниченных

сверху соответственно поверхностями z = 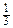(7 – x ² – y ²) и z = 1 + x ² + y ² => Рис.1.

V = V ₁ – V ₂ = 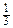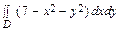– 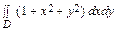. Переходя к полярным координатам, находим

V = – = – =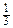

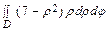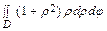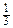
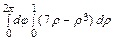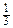
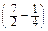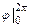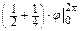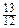· – = · 2 π – 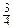· 2 π = 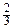π.