Пусть непрерывные функции х = j (u, v), у = y (u, v) осуществляют взаимно однозначное отображение области D * на область D и имеют непрерывные частные производные первого порядка. Пусть в области D на плоскости О х у задана непрерывная функция z = f (х, у). Каждому значению функции z = f (х, у) в области D соответствует равное значение функции
z = F (u, v) в области D *, где F (u, v) = f [ j (u, v), y (u, v) ].
Разобьем область D * на частичные области и построим соответствующее разбиение области D. Выберем в соответствующих частичных областях точки (u, v) и (х, у) так, чтобы значения функций F (u, v) и f (х, у) в них совпадали, и составим интегральные суммы для функций
f (х, у) и F (u, v) по областям D и D *. Получим
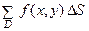 ≈
≈ 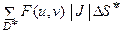 , (7)
, (7)
где Δ S ≈ | J | Δ S ٭и J = J (u, v) – якобиан функций j (u, v) и y (u, v). Переходя в равенстве (7) к пределу при стремлении к нулю наибольшего диаметра d * частичных областей Dk * (в силу непрерывности отображения (1) будет стремиться к нулю и наибольший из диаметров d частичных областей в D), будем иметь: 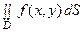 =
= 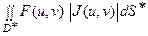 или
или
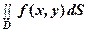 =
= 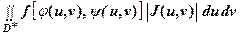 , (8)
, (8)
где J (u, v) = 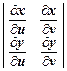 .
.
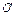
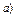





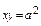
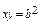
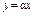
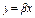



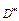
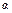
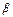
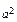
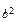
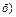 Т.о., для того чтобы преобразовать двойной интеграл, заданный в декартовых координатах, в двойной интеграл в криволинейных координатах, нужно заменить в подынтегральной функции f (х, у) переменные х и у соответственно через j (u, v) и y (u, v), а элемент площади dxdy - его выражением в криволинейных координатах: dxdy = | J | du dv.
Т.о., для того чтобы преобразовать двойной интеграл, заданный в декартовых координатах, в двойной интеграл в криволинейных координатах, нужно заменить в подынтегральной функции f (х, у) переменные х и у соответственно через j (u, v) и y (u, v), а элемент площади dxdy - его выражением в криволинейных координатах: dxdy = | J | du dv.
Пример 5. Найти площадь фигуры, ограниченной гиперболами ху = а 2 и
ху = b 2, где x > 0, y > 0, 0 < a < β, и прямыми у = αх и у = βx, 0 < α < β.
Введем новые криволинейные координаты ху = u, 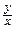 = v, которые
= v, которые
преобразуют фигуру D в плоскости Оху в прямоугольник
D ٭ = { a 2 ≤ u ≤ b 2; α ≤ v ≤ β } в плоскости O′uv (рис. 16).
Рис.16.
Имеем: x =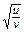 , y =
, y =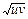 => J =
=> J = 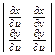 =
= 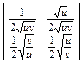 =
= 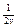 => S = || f (x, y) = 1 || =
=> S = || f (x, y) = 1 || =
= 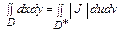 =
=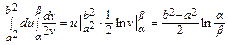 .
.
 2014-02-12
2014-02-12 2378
2378








