2014-02-12
821
Вычисление двойного интеграла часто упрощается заменой прямоугольных координат х и у полярными координатами r и j по формулам
x = r cos j, y = r sin j, где r ³ 0, 0 £ j £ 2 p. (9)
В этом случае J =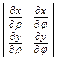 
= 
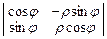= ρ.
Элемент площади в полярных координатах имеет вид dS = ρ dρ dφ, (10)
И формула перехода от интеграла в декартовых координатах к интегралу в полярных координатах можно записать так:
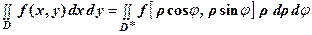. (11)
Т.о., чтобы преобразовать двойной интеграл в декартовых координатах в двойной интеграл в полярных координатах, нужно х и у в подынтегральной функции заменить соответственно через r cos j и r sin j, а элемент площади в декартовых коор-тах dxdy заменить элементом площади в полярных коор-тах r dr dj.
Как и в случае прямоугольных декартовых координат, вычисление интеграла в полярных координатах осуществляется путем сведения его к повторному интегралу, при этом пределы интегрирования по r и j области D * должны соответствовать пределам интегрирования по х и у области D.
Рассмотрим сначала случай, когда полюс О лежит вне заданной области D. Пусть область D обладает тем свойством, что любой луч, исходящий из полюса, пересекает ее границу не более чем в двух точках или по целому отрезку (рис. 17). Отметим крайние значения j 1 и j 2 полярного угла j, j 1 £ j £ j 2. Числа j 1 и j 2 являются пределами внешнего интегрирования.
|
|
|
Луч j = j 1 проходит через точку А контура области D,
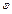
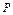
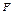
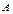
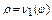
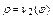а луч j = j 2 - через точку В. Точки А и В разбивают
контур области D на две части: АСВ и AFB. Пусть r = n 1 (j)
и r = n 2 (j) – их полярные уравнения, причем
n 1 (j) £ n 2 (j) для всех j Î j 1, j 2).
Функции n 1 (j) и n 2 (j) являются пределами внутреннего
интегрирования. Переходя к повторным интегралам, получаем
следующую формулу:
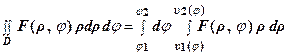. (12)
Рис. 17.
В частности, для площади S области D (при F (ρ, φ) ≡ 1) получаем
S =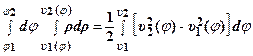 
.
Пусть теперь полюс О расположен внутри области D.
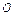
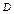
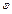
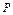
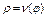
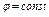Предположим, что область D является звездной, т.е. любой
луч j = const пересекает границу области только в одной
точке или по целому отрезку (рис. 18).
Пусть r = n (j) – уравнение границы области в полярных
координатах. Тогда Рис.18.
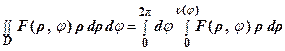. (13)
Замечание. Переход к полярным координатам полезен, когда
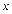
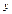
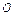
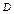подынтегральная функция имеет вид f (x 2 + y 2); область D
есть круг, кольцо или часть таковых.
Пример 7. Найти I =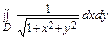 
по области D = { x 2 + y 2 ≤ 1, x ≥ 0, y ≥ 0} –
первой четверти единичного круга (рис.19). Рис.19.
Перейдем к полярным координатам: x = r cos j, y = r sin j =>
=> D → D ٭ =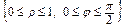 
=> I = || J = ρ || = 
= 
= 
= 
.
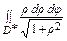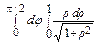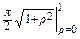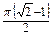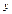
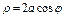
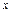Пример 8. Найти площадь фигуры, ограниченной кривой x 2 + y 2 = 2 ах.
 |
В полярных координатах уравнение данной кривой имеет вид:
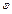r 2cos2 j + r 2sin2 j = 2 ar cos j ó r 2(cos2 j + sin2 j)= 2 ar cos j ó r 2 = 2 ar cos j ó
|
|
|
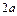
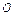
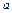
ó r = 2 a cos j. С другой стороны, x 2+ y 2= 2 ах ó x 2– 2 ах + y 2= 0ó x 2–2 ах + a 2+ y 2= a 2ó
ó (x – a)2 + y 2 = a 2 – окружность (рис. 20).
S =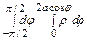 
=
=
= 
=
= 
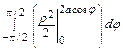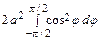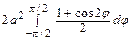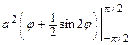= πa 2.
