Статическим моментомМх материальной точки массы m относительно оси Ох называется произведение mу, где у – ордината материальной точки, т.е. Мх = mу.
Здесь у может быть как положительным, так и отрицательным числом.
Разбивая фигуру D на части D 1, D 2,..., Dn, выбирая в каждой части Dk произвольно точку Рk (хk, уk) и считая, что масса этой k – той части приближенно равна m (хk, уk) D Sk и сосредоточена в точке Рk (хk, уk), запишем приближенно величину статического момента
фигуры D относительно оси Ох: Мх ≈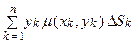 , где Δ Sk – площадь части Δ Dk, а
, где Δ Sk – площадь части Δ Dk, а
m (хk, уk) – поверхностная плотность.
Переходя к пределу при d → 0, получаем Мх = 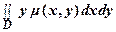 .
.
Статический момент фигуры D относительно оси Оу: Му = 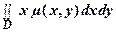 .
.
Если известны статические моменты Мх и Му и масса m плоской фигуры, то координаты центра тяжести:
хс = 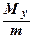 =
= 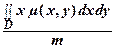 , ус =
, ус = 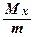 =
= 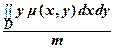 ,
,
Если μ = const, то m = μS, и
хс = 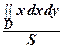 , ус =
, ус = 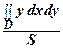 .
.
Пример 3. Найти массу, статические моменты Sx, Sy и координаты центра тяжести фигуры, лежащей в первой
четверти, ограниченной эллипсом 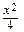 + y 2 = 1 и координатными осями. Поверхностная плоскость в
+ y 2 = 1 и координатными осями. Поверхностная плоскость в
каждой точке фигуры пропорциональна произведению координат точки.
|
|
|
По условию μ = μ (х, у) = kху, где k – коэффициент пропорциональности. Имеем:
m = 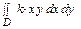 = k
= k 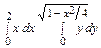 =
= 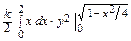 =
= 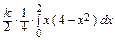 =
= 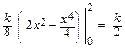 .
.
Sx = 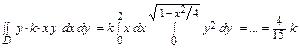 .
.
Sy = 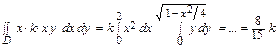 .
.
xc = 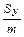 =
= 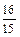 . yc =
. yc = 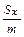 =
= 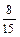 .
.
 2014-02-12
2014-02-12 1127
1127
