Если положить f (х, у) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой H = 1. Объем такого цилиндра численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
S = 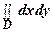 , или, в полярных координатах, S =
, или, в полярных координатах, S = 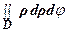 .
.
Масса плоской пластинки D с переменной плотностью γ = γ (х, у): m = 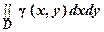 .
.
Если масса распределена равномерно по всей фигуре, γ = const, то: m =γ 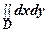 .
.
Пример 2. Найти массу кольца, ограниченного двумя концентрическими окружностями радиусов r и R, где
r < R, если плотность кольца в каждой точке обратно пропорциональна расстоянию от этой точки до
до центра окружности и равна 1 на окружности внутреннего круга.
D = { r ≤ ρ ≤ R, 0 ≤ φ ≤ 2 π }, γ = 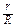 . m =
. m = 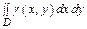 =
= 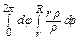 = 2 πr (R – r).
= 2 πr (R – r).
 2014-02-12
2014-02-12 2195
2195








