Лекция 20 Двудольные графы

11 12 13 14 15 16 17

Контрольные вопросы

1. Сформулировать определение эйлерова цикла (цепи).

2. Необходимое и достаточное условие существования Эйлерова цикла (цепи).Алгоритм построения эйлерова цикла (цепи).

3. Сформулировать определение гамильтонова цикла (цепи).

4. Необходимые и достаточные условия существования гамильтонова цикла (цепи).

5. Алгоритм выделения гамильтоновых циклов и цепей без учета инфомации о графе и с учетом информации.

ТЕМА: ДВУДОЛЬНЫЕ ГРАФЫ

ПЛАН:

1. Двудольный граф. Условие существования двудольного графа

2. Паросочетания. Реберные покрытия

Главная

1. Двудольный граф. Условие существования двудольного графа

V1 V2

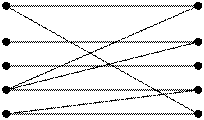Определение. Граф G(V, X) называется двудольным, если множество его вершин можно разбить на два подмножества V₁ и V₂ таких, что V = V₁ È V₂, V₁ Ç V₂ = Æ.Т.е. у любого ребра {v, w} Î X, если vÎ V₁, то w Î V₂. Множества V₁ и V₂ называются долями графа. На рисунке представлен типичный двудольный граф.

Двудольные графы играют заметнуя роль в различных приложениях. С помощью двудольных графов решаются такие задачи, как назначение на должность, определение степени соответствия товара требованиям покупателей и другие аналогичные задачи на соответствия.

Сформулируем задачу назначения на должность.

Имеется m человек и m должностей. Любой человек может занимать некоторые из должностей в соответствии со своей квалификацией. Вопрос: можно назначение на должность произвести таким образом, чтобы занятая каждым человеком должность не противоречила его квалификации.

Сформулируем еще одну задачу, решаемую с помощью двудольного графа. Это задача назначения комиссии из представителей n специальностей из людей, проживающих в m городах, таким образом, чтобы в комиссию вошли хотя бы по одному представителю каждой специальности и хотя бы по одному жителю из каждого города. Причем требуется составить комиссию с наименьшим количеством членов.

Условие существования двудольного графа формулируется в следующем утверждении, которое примем без доказательства.

Граф G(V, X) двудольный тогда и только тогда, когда все его простые циклы четной длины.

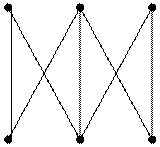
Если двудольный граф, в котором множеству V₁принадлежат m вершин, а множеству V₂ – n вершин, полный, то он обозначается К_m_,_n. Приведем пример графа К_3,3.

2. Паросочетания. Реберные покрытия

Задачи, сформулированные в предыдущем пункте, решаются путем отыскания в графе, так называемых, максимального паросочетания и минимального реберного покрытия. Сформулируем определения этих понятий.

Паросочетанием в М в графе G(V,X) называется подмножество ребер X' множества Х такое, что каждая вершина графа инцидентна не более чем одному ребру из X'.

Паросочетание с наибольшим числом ребер называется максимальным паросочетанием.

Реберным покрытием С графа G(V, X) называется такое подмножество его ребер X’ множества Х, что каждая вершина графа инцидентна хотя бы одному ребру из X’.

Реберное покрытие, содержащее наибольшее число ребер, называется минимальным реберным покрытием.

Рассмотрим граф, представленный на рисунке.

Паросочетаними являются множества: {{v₂, v₅}, {v₃, v₆}}, {{v₃, v₆}, {v₄, v₇}, {v₉, v₈}}. Максимальным паросочетанием является, например, множество {{v₈, v₄}, {v₆, v₃}, {v₅, v₂}}. Если в это множество добавить хотя бы одно какое- либо ребро, то это множество уже не будет паросочетанием.

Добавим в максимальное паросочетание ребра {v₁, v₂}, {v₄, v₇}, {v₉, v₈}, получим реберное покрытие, причем минимальное.

Задачи о максимальном паросочетании и минимальном реберном покрытии связаны между собой таким образом, что решение любой из них позволяет найти решение другой. Изучим связь между этими задачами.

1. Пусть М – произвольное паросочетание графа. Возьмем любую вершину vÎ V, которая не инцидентна ни одному из ребер, составляющих М. добавим к паросочетанию любое ребро, инцидентное вершине v, и будем повторять это действие до тех пор, пока не переберем все вершины, не инцидентные ни одному ребру из М. в результате получим множество ребер C'Í Х, являющихся реберным покрытием графа.

2. Пусть С – произвольное реберное покрытие, вершина vÎ V, инцидентна более чем одному ребру из С. Исключим из С любое инцидентное v ребро и будем повторять это действие до тех пор, покане останется ни одной вершины, которая инцидентна более чем одному ребру. Получим некоторое паросочетание M’ графа G.

Справедливо утверждение, которое примем без доказательства:

Если М – максимальное паросочетание, то C' – минимальное реберное покрытие. Если С – минимальное реберное покрытие, то М' – максимальное паросочетание.

Эквивалентность задач о максимальном паросочетании и минимальном реберном покрытии позволяет при решении одной из них построить и решение другой.

Введем несколько необходимых понятий.

Открытая вершина – это вершинане инцидентная ни одному ребру из ребер паросочетания М.

Чередующаяся цепь – это простая цепь, в которой из любой пары смежных ребер одно принадлежит М, а другое – не принадлежит.

Увеличивающая чередующаяся цепь – это чередующаяся цепь, у которой концевые вершины являются открытыми.

Для графа, представленного на рисунке выше возьмем паросочетание М = {{v₂, v₅}, {v₃, v₆}}, тогда упорядоченная последовательность ребер {{v₁, v₂}, {v₂, v₅}, {v₅, v₆}, {v₆, v₃}, {v₃, v₄}} - увеличивающая чередующаяся цепь.

Алгоритм выделения максимального паросочетания основывается на утверждении:

Паросочетание М тогда и только тогда максимальное, когда для него не существует увеличивающей чередующейся цепи.

Алгоритм построения максимального паросочетания

Задан связный граф G(V, X) и выделено какое – либо паросочетание М:

выбрать любую открытую вершину и отыскать увеличивающую чередующуюся цепь;
если такая цепь есть, то не входившие в паросочетания ребра этой цепи включить в максимальное паросочетание, а остальные исключить;
если для выбранной вершины не найдется такая цепь, то выбрать другую вершину и повторить работу;
алгоритм заканчивается, когда все открытые вершины прверены на наличие увеличивающей цепи.

Минимальное реберное покрытие можно получить из построенного максимального паросочетания следующим образом: взять любую вершину, не инцидентную ребрам из М.; добавить к паросочетанию любое ребро, инцидентное этой вершине и повторять действие до тех пор, пока не переберем все вершины, не инцидентные ни одному ребру из М.

Рассмотрим пример на построение максимального паросочетания и минимального реберного покрытиядл вышеприведенного графа:

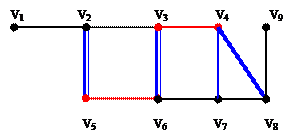
выделим паросочетание { {v₅, v₆},{v₃, v₄}} (ребра окрашены в красный цвет);
открытыми являются вершины: v₁, v₂, v₇, v₈, v₉;
для вершин v₂, v₇, v₈ существуют увеличивающие цепи;
для v₂: {v₂, v₅}, {v₅, v₆}, {v₆, v₃}, {v₃, v₄}, {v₄, v₇}; для нее максимальное паросочетание: {v₂, v₅}, {v₆, v₃}, {v₄, v₇} (ребра – синие тонкие линии));
для v₇ – как для v₂;
для v₈ максимальное паросочетание: {v₈, v₄}, {v₃, v₆}, {v₅, v₂} (ребра – широкие синие линии).

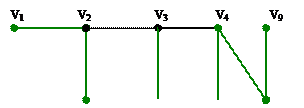
Из максимального паросочетания, например для вершины v₂, построим минимальное реберное покрытие: не инцидентны вершины v₁ и v₈. Добавим ребра к М: {v₁, v₂}, {v₈, v₄}. Осталась не инцидентной вершина v₉. Добавим в построенное реберное покрытие еще одно ребро {v_9,v₈}.

М вместе с добавленными ребрами – минимальное реберное покрытие данного графа.