ТЕМА: ОРИЕНТИРОВАННЫЙ ГРАФ
ПЛАН:
- Основные понятия
- Способы задания ориентированного графа
- Путь в ориентированном графе
- Связность. Компоненты связности в орграфе
Главная
- Основные понятия
Напомним определение ориентированного графа:
Непустое множество V = {v1, v2,…,vn} и набор Х упорядоченных пар объектов (vi, vi+1), где viÎV, vi+1ÎV, называется ориентированным графом и обозначается D(V, X).
Пары х = (v, w) называются дугами и изображаются на диаграмме следующим образом:

v– начало дуги х, w – конец дуги х.
Говорят: дуга исходит из v и заходит в w.
Пусть х – дуга. Если v конец или начало дуги, то v и х инцидентны.
Вершины v и w смежны, если (v, w) Î X.
Для ориентированного графа аналогично определяются понятия: петли, кратные дуги, псевдограф, мультиграф, граф.
Рассмотрим понятия: полустепень исхода и полустепень захода:
Полустепенью исхода вершины v называется число d+(v) дуг орграфа D, исходящих из вершины v.
Полустепенью захода вершины v называется число d-(v) дуг орграфа D, заходящих в вершину v.
Замечание: вклад каждой петли, инцидентной некоторой вершине v, равен 1, как в d+(v), так и в d-(v).
Для орграфа, представленного на рисунке найти полустепени захода и исхода:
|

d+(u1) = 2
d-(u1) = 0
d+(u2) = 2
d-(u2) = 3
d+(u3) = 0
d-(u3) = 1
d`+(u4) = 0
Найдем суммы степеней исходов и сумму степеней заходов:
еd+(u) = 2 + 2 + 0 + 0 = 4;
еd-(u) = 0 + 3 + 1 = 4.
В данном графе 4 ребра. Замечаем, что еd+(u) = еd+(u) = m.Действительно, для орграфа справедливо утверждение:
Для любого ориентированного графа выполняется равенство
еd+(u) = еd+(u) = m,
где m – количество дуг.
- Способы задания ориентированного графа
Ориентированный граф как и неориентированный можно задать с помощью его диаграммы или в матричной форме.
Матрица инцидентности графа.
Пусть задан граф D(V, X), где V ={v1, v2, …, vn}, X = {x1, x2,…, xm}.
Матрицей инцидентности графа D(V, X) называется матрица размера m´ n, элементы которой определяются следующим образом:
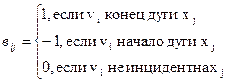
Замечание: если хj – петля для vi, то bij – любое число, отличное от 1, -1 и 0.
Матрица инцидентности однозначно определяет структуру графа, что позволяет читать всю необходимую информацию о графе. Информация о дугах считывается по строкам, о вершинах – по столбцам.
Составим матрицу инцидентности для орграфа из предыдущего примера. Это матрица размера 4´ 4:
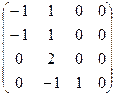
Элемент b32 = 2 показывает, что дуга х3 является петлей. Найдем полустепени исхода и захода, например, для вершины v2: полустепень исхода - d+(v2) = 2, т.к. в соответстующем этой вершине столбце одна «-1» и еще учитываем петлю; полустепень захода - d-(v2) = 3, т.к в столбце две единицы и петля.
Матрица смежности
Пусть задан граф D(V, X), где V ={v1, v2, …, vn}, X = {x1, x2,…, xm}.
Матрицей смежности графа D(V, X) называется квадратная матрица n´ n, элементы которой определяются следующим образом:
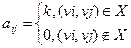
k – количество дуг, соединяющих вершины vi и vj.
Составим матрицу смежности для орграфа. Это квадратная матрица размера 4´ 4:
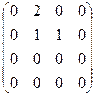
Матрица смежности ориентированного графа не симметрична относительно главной диагонали, как матрица смежности для неорграфа.
3. Путь в ориентированном графе
Определение: Путем, соединяющим вершины v1 и vk+1, называется последовательность v1x1v2x2…vkxkvk+1, где k³ 1, vi Î V, xiÎ X, дуга xi соединяет вершины vi с вершиной vi+1. Вершина v1 (v нач)– начало пути (начальная вершина), vk+1 (v кон)– конец пути (конечная вершина). Остальные вершины называются внутренними вершинами пути.
Найдем какой-либо путь из v1 в v3: v1x1v2x3v2x4v3.
Допускается краткая запись пути. В том случае, если в пути нет кратных дуг, то составляют последовательность только из вершин.
Если в пути есть кратные дуги, то в последовательность включают начальную вершину, дуги и конечную вершину. Или пользуются комбинированной записью: в последовательность включают все вершины и только кратные ребра.
Перепишем наш путь, использую комбинированную запись: v1x1v2v2v3. В последовательность включено только кратное ребро x1.
Длиной пути l называется количество дуг в нем.
В нашем пути 3 дуги, значит его длина l =3.
Познакомимся с видами путей.
Если vнач = vкон, то путь называется замкнутым.
Если vнач ¹ vкон, то путь называется незамкнутым.
Виды незамкнутых путей:
Незамкнутый путь, в котором все дуги попарно различны называется цепью.
Цепь, в которой все вершины попарно различны называется простой цепью.
Виды замкнутых путей:
Замкнутый путь, в котором все дуги попарно различны называется контуром.
Контур, в котором все вершины попарно различны называется простым контуром.
Заметим, что петля являются простым контуром.
Составим различные пути для приведенного выше орграфа:
v1x1v2x3v2x4v3 – незамкнутый путь, являющийся цепью (в нем все дуги попарно различны);
v2x3v2 – простой контур;
v1x2v2x4v3 – простая цепь (все вершины и дуги попарно различны).
Для графа D(V,X) справедливы утверждения:
Из любого контура можно выделить простой контур.
Из любого незамкнутого пути можно выделить простую цепь с теми же начальной и конечной вершинами.
 2014-02-12
2014-02-12 2238
2238








