Лекция 21 Плоские графы

Контрольные вопросы

1. Какой граф называется двудольным.
2. Перечислить перечень некоторых задач на двудольные графы.
3. Условие существования двудольного графа.
4. Что называется паросочетанием и максимальным паросочетанием?
5. Что называется реберным покрытием и минимальным реберным покрытием?
6. Связь между задачами о выделении паросочетания и реберного покрытия.
7. Пояснить понятия – открытая вершина, чередующаяся цепь и увеличивающая цепь.
8. Рассказать алгоритм выделения максимального паросочетания и минимального реберного покрытия.

ТЕМА: ПЛОСКИЕ ГРАФЫ

ПЛАН:

1. Задача о плоской укладке графа

2. Основные определения

3. Алгоритм плоской укладки графа

Главная

1. Задача о плоской укладке графа

Имеется много приложений задачи о плоской укладке графа. Одним из характерных является проблема размещения на печатных платах приборов различных радиоэлектронных устройств. Приборы (резисторы, трансформаторы, конденсаторы и т.д.) должны быть размещены на плате таким образом, чтобы гальванические соединения, осуществляемые с помощью частей проводящего слоя платы, полностью соответствовали принципиальной схеме устройства. При этом должно быть соблюдено требование: проводники пересекаются лишь в контактах платы.

Если представить приборы: вершины графа, а гальванические связи между ними – ребра графа, то задача размещения приборов сводится к такому изображению графа на плоскости, при котором никакие два ребра не пересекаются.

При большом числе приборов и гальванических соединений между ними задача представляется довольно сложной.

2. Основные определения

Граф G(V, X) укладывается на поверхности, если его можно на ней изобразить таким образом, что любое пересечение его ребер является вершиной графа.

Если граф укладывается на плоскости, то он называется планарным.

Граф, уложенный на плоскости называется плоским графом.

Плоский граф на плоскости определяет ее области. При этом неограниченная область называется внешней гранью графа, а остальные области – внутренние грани. Внешнюю грань обозначим S₀, а внутренние S₁, S₂, …, S_k. На рисунке представлен планарный граф и соответствующий ему плоский граф с гранями:

Для плоских графов справедлива формула Эйлера: n + k = m + 2, где n – число вершин графа, k – число граней, m – число ребер.

Для представленного графа: число вершин равно 5, число ребер – 8, число граней – 5. проверим формулу Эйлера:

5 + 5 = 8 – 2 – равенство верно.

Вопрос о распознавании планарности графа являлся в свое время серьезной математической проблемой, которую на сегодняшний день удалось решить.

Для формулировки этого важного результата введем два понятия.

Элементарное стягивание ребра. Элементарным стягиванием ребра {v, w} называется отождествление вершин v и w:

 

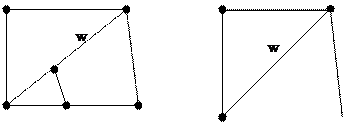Два графа G' и G'' называютя гомеоморфными, если они могут быть получены из некоторого графа с помощью последовательности элементарных стягиваний его ребер.

Выше приведенные графы гомеоморфны. Никакие другие вершины стягивать нельзя, так как это повлечет за собой отождествление ребер, что недопустимо.

Сформулируем необходимое и достаточное условие планарности графа.

Для того чтобы граф G(V, X) был планарным, необходимо и достаточно, чтобы он не содержал подграфа, гомеоморфного либо полному графу К₅, либо графу К_3,3.

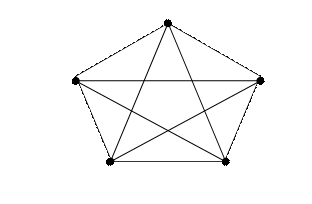
Граф К₅

3. Алгоритм плоской укладки графа

Изложим алгоритм, с помощью которого устанавливается возможность получения плоской укладки графа, если он является планарным, и невозможность укладки в противном случае.

Пусть даны граф G(V, X) и его подграф Этот подграф называется начальным и должен быть планарным (в качестве такого подграфа можно взять простой цикл, простую цепь). Через G'(V', X') обозначим подграф графа G, порожденный удалением из него вершин (напомним, что при удалении вершины удаляются и все инцидентные ей ребра). Пример представлен на рисунке.

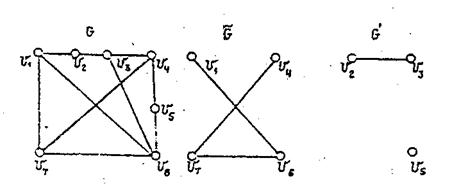
Граф G' может быть не связным, т.е. иметь Р компонент связности. Обозначим компоненты связности G'_i(V’_i, X’_i), где i =1 – р. Множество ребер X’_I дополним всеми ребрами, инцидентными в G вершинам V’_i, а множество вершин V’_i дополним соответствующими вершинами этих ребер и назовем их контактными вершинами. Полученный таким образом подграф 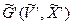назовем куском графа G относительно подграфа 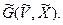Объединением всех кусков графа должен быть исходный граф G. На рисунке представлены куски данного графа, относительно подграфа

Грань, определяемую графом на плоскости, и кусок назовем совместимыми, если все контактные вершины куска являются граничными точками этой грани.

Алгоритм плоской укладки графа состоит в последовательном присоединении к любому уже уложенному подграфу графа G простой цепи L, обе концевые вершины которой - единственные ее вершины, принадлежащие уложенному графу. Выбор простой цепи осуществляется после того, как будет проанализирована совместимость каждого куска и граней уложенного графа. При анализе совместимости возможны варианты:

1. кусок совместим с единственной гранью;

2. каждый кусок совместим более чем с одной гранью;

3. существует кусок, с которым каждая грань уложенного подграфа несовместима.

В первом случае в куске находится простая цепь, обе концевые вершины которой (и только они) являются вершинами уложенного подграфа, и эта цепь укладывается в совместимую грань.

Во втором случае простая цепь выбирается в любом из кусков и выполняется такое же действие, как и в первом случае.

Третий случай говорит о том, что граф G не является планарным.

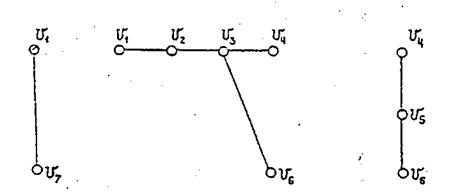
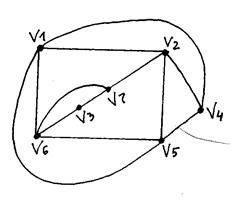
Рассмотрим работу алгоритма при получении плоской укладки графа, изображенного на рисунке

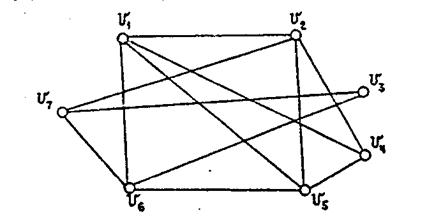
1. В качестве начального планарного подграфа возьмем простой цикл v₁ v₂ v₅ v₆ v₁, и обозначим его . Удалим все вершины этого подграфа и получим подграф G'(V', X') c двумя компонентами связности:

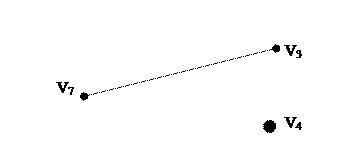
2. Получим два куска, дополняя каждую компоненту связности графа G'(V', X'), и добавляя ребро {v₁, v₅}:

	V6

 

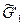
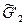
3. Начинаем плоскую укладку. Простой цикл образует две грани:

	V1		V1

 

Заполним таблицу:

Вершины куска	Контактные вершины	Совместимые грани
v1, v5	v1, v5	S0, S1
v3, v7, v2, v6	v2, v6	S0, S1
v4, v1, v2, v5	v1, v2, v5	S0, S1

4. Все куски совместимы с двумя гранями. Возьмем ребро {v₁, v₅} и уложим его в грани S₀, которая разбивается на две грани S₂ и S₃.

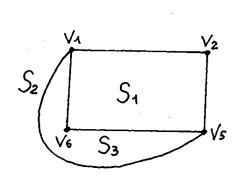
Вершины куска	Контактные вершины	Совместимые грани
v3, v7, v2, v6	v2, v6	S1
v4, v1, v2, v5	v1, v2, v5	S1, S2

5. Рассмотрим первый кусок, который совместим только с гранью S₁. Выбираем в нем простую цепь v₂ v₇ v₃ v₆ и укладываем ее в грани S₁, которая разбивается на две грани S₄ и S₅.

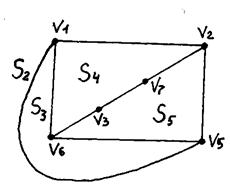
Вершины куска	Контактные вершины	Совместимые грани
v7, v6	v7, v6	S4, S5
v4, v1, v2, v5	v1, v2, v5	S2

6. Первый кусок совместим с двумя гранями. Поместим ребро {v₆, v₇} в грань S₄, она разбивается на две новые грани S₆ и S₇.

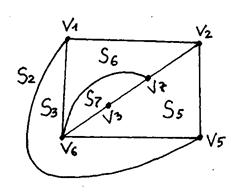
Вершины куска	Контактные вершины	Совместимые грани
v4, v1, v2, v5	v1, v2, v5	S2

7. Имеем один кусок, который совместим с единственной гранью. Выделяем в нем простую цепь v₅ v₄ v₁ и укладываем ее в грань S₂, разбивая ее на грани S₈, S₉.

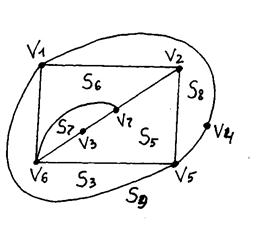
Вершины куска	Контактные вершины	Совместимые грани
v4, v2	v4, v2	S8

8. Последний кусок совместим с гранью S₈, значит граф планарный. Укладываем ребро {v₂, v₄} в грань S₈, заканчивая плоскую укладку графа.

Контрольные вопросы

1. Какой граф называется планарным и плоским?
2. Какие области определяет плоский граф на поверхности?
3. Какие вершины называются контактными?
4. Что такое кусок графа? В каком случае кусок графа и грань графа совместимы.
5. Какое равенство справедливо для планарного графа?
6. Сформулировать алгоритм плоской укладки графа.