Лекция 19. 1. Какой маршрут называется минимальным

Контрольные вопросы

1. Какой маршрут называется минимальным?

2. Алгоритм выделения минимального маршрута в ненагруженном неорграфе.

3. Алгоритм выделения минимального маршрута в нагруженном графе.

4. Какой граф называется ациклическим? Какой подграф называется остовом? Алгоритм его построения.

5. Что называется цикловым рангом графа? Что такое цикломатическое число, цикловой базис графа? Алгоритм построения циклового базиса графа.

ТЕМА: ЭЙЛЕРОВЫ И ГАМИЛЬТОНОВЫ ЦЕПИ И ЦИКЛЫ

ПЛАН:

1. Эйлеровы цепи и циклы

2. Гамильтоновы циклы и цепи

Главная

1. Эйлеровы цепи и циклы

Классической в теории графов является следующая задача. В городе Кенигсберге имеется два острова, соединенных семью мостами с берегами реки Преголь и друг с другом, как показано на рисунке.

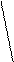
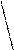
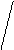
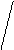
Задача состоит в следующем: осуществить прогулку таким образом, чтобы, пройдя по одному разу по каждому мосту, вернуться обратно. Решение этой задачи сводится к поиску некоторого специального маршрута.

Пусть G(V, X) – псевдограф. Цепь (цикл) в G(V, X) называется эйлеровой (эйлеровым), если она (он) проходит по одному разу через каждое ребро графа G(V, X).

Поставим в соответствие схеме мультиграф, в котором каждой части суши соответствует вершина, а мостам – ребра. На языке теории графов задача прозвучит так: найти эйлеров цикл в мультиграфе G(V, X).

V1

V2

V3

V4

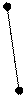
Прежде чем решать задачу о выделении эйлерова цикла или эйлеровой цепи, очевидно нужно выяснить, существуют ли они. Необходимым условием существования эйлерова цикла или цепи является связность графа.

Ответы на вопросы о существовании в графе эйлерова цикла и цепи дают ниже приводимые утверждения. Для их доказательства понадобятся вспомогательные утверждения.

Если в псевдографе G имеется хотя бы одно ребро и отсутствуют висячие вершины, то G содержит хотя бы один простой цикл.

Доказательство проведем по индукции.

Пусть G содержит только одно ребро, тогда это ребро – петля, т.к. нет висячих вершин, а петля – это простой цикл.

Пусть G содержит два ребра, тогда это кратные ребра. И, следовательно, простым циклом является v x₁ w x₂ v:

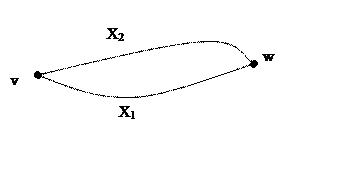
Пусть граф не содержит кратных ребер, т.е G – граф и v₁, v₂ – произвольные смежные вершины графа. Рассмотрим последовательность v₁, v₂, v₃…вершин графа G такую, что для любого i ³ 3 вершины v_i, v _i-1 смежны и v_i ¹ v_i-2:

	vi-2 vi-1 vi

Поскольку в графе нет висячих вершин, то такую последовательность можно продолжать неограниченно. Используя конечность множества вершин графа, получаем, что обязательно произойдет совпадение v_i = v_j, где 1£ i < j – 2. Пусть это будет первое совпадение, т.е. совпадение с наименьшим номером j. Тогда последовательность v_i v _i+1 v _i+2…v_j – простой цикл в графе.

Введем обозначения: если m₁ и m₂ – циклы псевдографа G, имеющие хотя бы одну общую вершину и не имеющие общих ребер, то, очевидно, существует цикл, проходящий через все ребра, входящие в m₁ и m₂. Обозначим m₁ + m₂ любой из таких циклов. Для любого цикла обозначим V(m) и X(m) соответственно множество вершин и множество ребер, входящих в m.

Пусть m - цикл без петель. Тогда для "v Î V(m) количество ребер в Х(m), инцидентных v, четно.

Поскольку в цикле m отсутствуют петли и все ребра попарно различны, то с каждым новым вхождением в m вершины v в этот цикл войдут также два новых инцидентных ей ребра, а следовательно, общее число ребер в Х(m) инцидентных v, четно.

Следствие. Если вершина входит в некоторый цикл. То она не может быть висячей.

Теперь сформулируем и докажем теорему о существовании в графе эйлерова цикла.

Для того, что бы связный псевдограф G обладал эйлеровым циклом, необходимо и достаточно, что бы степени его вершин были четными.

Необходимость. Пусть G обладает эйлеровым циклом.

Удалим из G все петли. Получим мультиграф G’, который также обладает эйлеровым циклом. Т.к эйлеров цикл мультиграфа G' содержит все ребра из G', а следовательно, и все вершины из G', то в силу утверждения 2 степени всех вершин мультиграфа G' четны, откуда, учитывая то, что вклад петли в степень вершины, инцидентной этой петле, равен 2, получаем четность степеней всех вершин графа G.

Достаточность. Пусть m – количество ребер в G.

При m = 1 связный псевдорграф G с вершинами четной степени может выглядить только следующим образом: G(V, X), где V = {v}, X = {x = {v, v}}. Значит, G(V, X) – петля, а петля – это эйлеров цикл.

Предположим, что для некоторого целого m ³ 2 достаточность доказана для всякого псевдографа с m -1 ребрами. Докажем справедливость для псевдографа с m ребрами.

Пусть в связном псевдографе G c m ребрами степени вершин четны. В силу утверждения 1 в G имеется простой цикл m₀. Если m₀ содержит все ребра из G, то эйлеров цикл найден. В противном случае удаляем из G все ребра, содержащиеся в m₀. в результате получим псевдограф G', каждая компонента связности которогоявляется либо изолированной вершиной, либо псевдографом, степень каждой вершины которого четна. Пусть G_i, где i = 1, 2, …р – компоненты связности графа G',отличные от изолированных вершин. По предположеню, для каждого псевдографа G_i можно построить эйлеров цикл m_I. В силу связности G цикл m₀ имеет общие вершины с любым из циклов m_i, где i = 1, 2, …р. Тогда искомым эйлеровым циклом в G является цикл:

m = (…((m₀ + m₁) + m₂) + …+ m_р).

Сформулируем и докажем теорему о существовании эйлеровой цепи в графе.

Для того, что бы связный псевдограф G обладал эйлеровой цепью, необходимо и достаточно, что бы он имел ровно две вершины нечетной степени.

Необходимость. Пусть G имеет эйлерову цепь, соединяющую v и w. Добавим к G дополнительное ребро {v, w}. Получим псевдограф G', обладающий эйлеровым циклом, а следовательно, степени вершин графа G' четны. Но тогда четны и степени вершин псевдографа G, за исключением вершин v и w.

Достаточность. Пусть G имеет ровно две вершины v и w нечетной степени. Добавим к G новое ребро {v, w}. Получим связный псевдограф G' со всеми вершинами четной степени. Тогда в графе G' существует эйлеров цикл. Исключив из этого цикла ребро {v, w}, получим эйлерову цепь, соединяющуя вершины v и w.

Замечание. Эйлерова цепь соединяет вершины нечетной степени. Вернемся к задаче о Кенигсбергских мостах. Необходимое условие существования эйлерова цикла или эйлеровой цепи выполняется, т.к граф связный. Найдем степени вершин графа: d(v₁) = d(v₂) = d(v₄) = 3, d(v₃) =5. Значит, граф не обладает ни эйлеровым циклом, ни эйлеровой цепью.

Познакомимся с алгоритмами выделения эйлерова цикла и эйлеровой цепи.

Алгоритм 1 выделения эйлерова цикла в связном мультиграфе G(V,X), где Х ¹Æ и степени вершин четны..

1. Выделить из G цикл m₁. Положить k = 1 (k - число циклов), G' = G.

2. Удалить из G' ребра, принадлежащие множеству Х(m_k). Полученный псевдограф снова обозначить G'. Если в G' отсутствуют ребра, то переходим к шагу 4. В противном случае выделяем из G' цикл m_k+1 и перейти к шагу 3.

3. Присвоить k: = k + 1 и перейти к шагу 2.

4. По построению m₁, …, m_k – циклы. Если k = 1, то m₁ – искомый эйлеров цикл, работа алгоритма заканчивается. В противном случае находим цикл m_i такой, что V(m_i) Ç V(m₁) ¹Æ, где 2 £ i £ k. Перейти к шагу 5.

5. Присвоить к: = i – 1, m₁: m₁ + m_i, m_j: m_j+1 , j = I, …, k. Перейти к шагу 4.

Применим этот алгоритм для выделения эйлерового цикла для псевдографа с четными степенями вершин..

Удалим из G петли. Получим связный мультиграф G’, степени которого четны. Пусть в G’ имеется хотя бы одно ребро. Тогда, применяя к G' приведенный алгоритм, найдем эйлеров цикл в графе G'. Добавляем в этот цикл удаленные петли, получим эйлеров цикл в G.

Рассмотрим теперь применения этого алгоритма для выделения эйлеровой цепи в связном псевдографе, имеящим ровно две вершины v, w нечетной степени., где Х ¹Æ. Добавляя к G ребро {v, w}, получим псевдограф G' с четными степенями вершин. Выделив в G' эйлеров цикл и удалив из него ребро {v, w}, получим эйлерову цепь.

Алгоритм 2 выделения эйлерова цикла в связном мультиграфе G(V,X), где Х ¹Æ и степени вершин четны.

1. Выбрать произвольно некоторую вершину v.

2. Выбрать произвольно некоторое ребро х, инцидентное v, и присвоить ему номер 1.

3. Каждое пройденное ребро вычеркивать и присваивать ему номер, на единицу больший номера предыдущего вычеркнутого ребра.

4. Находясь в вершине v_i, не выбирать ребра, соединяющего v_i с v, если есть возможность другого выбора.

5. Находясь в вершине v_i, не выбирать ребра, которое является мостом (при удалении которого граф, образованный незачеркнутыми ребрами, распадается на две компоненты связности, имеющие хотя бы по одному ребру).

6. После того, как в графе будут занумерованы все ребра, цикл, образованный ребрами с номерами от 1 до n, где n – число ребер в графе, есть эйлеров цикл.

Для использования этого алгоритма для построения эйлеровой цепи первый пункт будет таким: выбрать вершину с нечетной степенью. Остальные шаги не изменятся.

Пример. Построить эйлеров цикл, используя оба алгоритма.

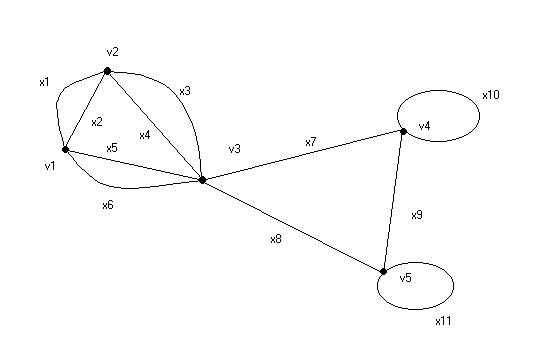
Применим первый алгоритм.

Данный псевдограф - связный. Найдем степени вершин: d(v₁) = 4, d(v₂) = 4, d(v₃) = 6, d(v₄) = 4, d(v₅) = 4. Все степени вершин четные, следовательно, граф обладает эйлеровым циклом. Построим его.

Используем первый алгоритм.

Удалим петли х₁₀ и х₁₁. Получим мультиграф. Выделим цикл v₃x₄x₂x₅v₃ – обозначим m₁. Удалим ребра x_4, x_2, x₅. Снова выделяем цикл v₃x₃x₁x₆v₃ - m₂ . V(m₁)ÇV(m₂) = {v₁, v₂, v₃}. Удалим ребра. Выделяем цикл v₃x₇x₉x₈v₃ - m₃. V(m₂)ÇV(m₃) = {v₃}. В мультиграфе построили эйлеров цикл m_{1 +} m₂ + m₃ . Добавим удаленные петли и получим цикл в заданном графе: v₃x₄x₂x₅ x₃x₁x₆ x₇ x₁₀ x₉ x₁₁ x₈v₃.

Используем второй алгоритм.

Как и в первом алгоритме, удалим петли, получим мультиграф. Выберем любую вершину, например, v₃. Выберем инцидентное ей ребро, например, х₇. Присвоим ему номер 1, т.е. х₇₁ и вычеркнем. Выбираем инцидентное ребро вершине v₄ – это ребро х₉, присвоим ему номер 2 – х₉₂, вычеркнем. Выбираем инцидентное ребро вершине v₅ – это ребро х₈, присвоим ему номер 3 – х₈₃, вычеркнем. Далее аналогичным образом выбираем ребра х₄, х₂, х₅ и х₃, х₁, х₆. В мультиграфе эйлеров цикл построен. Добавим в него удаленные петли. Окончательно получим эйлеров цикл в данном графе: v₃x₇x₁₀x₉ x₁₁x₈x₄ x₂ x₅ x₃ x₁ x₆v₃.

2. Гамильтоновы циклы и цепи.

Пусть G— псевдограф. Цепь (цикл) в Gназывается гамильтоновой (гамильтоновым), если она (он) проходит через каждую вершину псевдографа G ровно один раз.

С понятием гамильтоновых циклов тесно связана так назы­ваемая задача коммивояжера: в нагруженом графе G опреде­лить гамильтонов цикл минимальной длины (иными слова­ми, коммерсант должен совершить поездку по городам и
вернуться обратно, побывав в каждом городе ровно один paз, и при этом стоимость такой поездки должна быть мини­мальной.

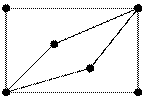
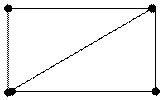
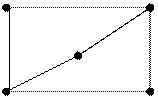
На первый взгляд, понятие гамильтонова цикла сходно c понятием эйлерова цикла. Приведенные в таблице графы, где первый столбец соответствует случаям существования, второй столбец – не существования гамильтоновых циклов, а строки – случаям существования (первая строка и не существования (вторая строка) эйлеровых циклов, показывают независимость этих понятий.

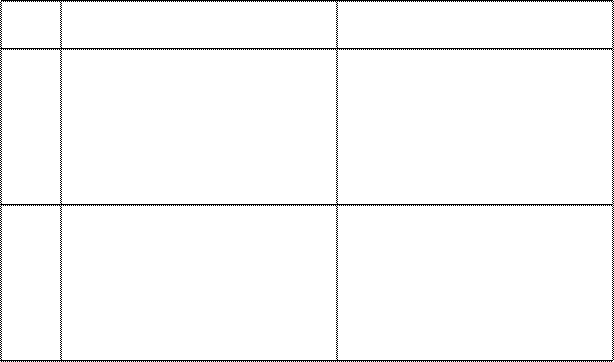
1 2

Приведем необходимые и достаточные условия существования гамильтоновых циклов и цепей.

Рассмотрим класс графов, в которых заведомо суще­ствуют гамильтоновы цепи и циклы – это полные графы. Очевидно, что в полном графе всегда существуют гамильтонов цикл, а также гамильтоновы цепи, соединяющие две произ­вольные вершины этого графа, т.к. любая вершин полного графа смежна со всеми остальными вершинами Таким образом, простейшим до­статочным условием существования гамильтоновых цепей и цик­лов в графе является его полнота. Приведем также простейшие необходимые условия. Очевидным необходимым условием суще­ствования гамильтоновых цепей и циклов в графе G является связность G. Более тонким необходимым условием существова­ния гамильтонова цикла в графе Gявляется следующее утверждение (примем его без доказательства):

Если граф G обладает гамильтоновым циклом, то в нем отсутствуют точки сочленения.

Приведем наиболее простые методы выделения в графе G(V,X), где V = {v₁, …, v_n}, гамильтоновых циклов и цепей. Наиболее простым из них является метод перебора всевозможных перестановок v_i1, …, v_in множества V. Если перестановка является маршрутом в G, то эта перестановка – гамильтонова цепь. По окончании перебора всех возможных перестановок будут выделены все гамильтоновы цепи.

Для выделения гамильтоновых циклов перебираем всевозможные перестановки v₁, v_i1, …, v_in-1. Если v₁, v_i1, …, v_in-1, v₁ – маршрут в графе G, то это гамильтонов цикл.

При выделении всех гамильтоновых цепей необходимо перебрать n! Перестановок, при выделении гамильтоновых циклов – (n – 1)! перестановок.

Описанный метод не учитывает информацию о графе. Рассмотрим метод, аналогичный предыдущему, но учитывающий информацию о графе. Составим всевозможные последовательности вершин v_i1, …, v_ir, где v_i1 Î V, v_i2 Î G(v_i1)\{v_i1}, …, v_ir Î G(v_ir-1)\{v_i1, …, v_ir-1}, G(v_ir) \{v_i1, …, v_ir}= Æ, где G(v_ir) – множество образов вершины v_ir. Тогда в каждом случае, когда r = n, последовательность v_i1, …, v_ir – гамильтонова цепь. Соответственно, когда r = n, v_i1 Î G(v_in), последовательность v_i1, …, v_ir, v_i1 – гамильтонов цикл.

При этом выделяются все гамильтоновы циклы и цепи.