Задания для самостоятельной работы
Лекция 13. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-ГО ПОРЯДКА, ПРИВЕДЕНИЕ ИХ К КАНОНИЧЕСКОМУ ВИДУ И НАХОЖДЕНИЕ ОБЩЕГО РЕШЕНИЯ
Рассмотрим уравнение
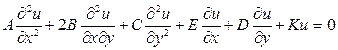 , (13.1)
, (13.1)
которое можно также записать в виде
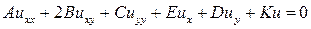 , (13.1*)
, (13.1*)
и уравнение
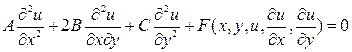 , (13.2)
, (13.2)
которое можно также записать в виде
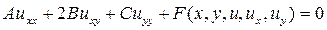 , (13.2*)
, (13.2*)
где u – искомая функция х и у; A, B, C, E, D, K – коэффициенты, которые могут быть как функциями х и у, так и постоянными величинами, некоторые из которых могут быть равные нулю.
Уравнение (13.1) или (13.1*) называется линейным, а уравнение (13.2) или (13.2*) называется квазилинейным, поскольку оно линейно только относительно старших производных, входящих в это уравнение.
Линейные уравнения в частных производных классифицируются на три типа:
- линейные уравнения гиперболического типа (ГТ);
- линейные уравнения параболического типа (ПТ);
- линейные уравнения эллиптического типа (ЭТ).
Для того, чтобы классифицировать уравнения в частных производных необходимо проанализировать выражение
В 2 – АС,
состоящее из коэффициентов при старших производных в уравнениях (13.1) - (13.2*).
Если В 2 – АС > 0, то исходное уравнение будет принадлежать к уравнениям ГТ.
Если В 2 – АС = 0, то исходное уравнение будет принадлежать к уравнениям ПТ.
Если В 2 – АС < 0, то исходное уравнение будет принадлежать к уравнениям ЭТ.
Определим, к какому типу принадлежат волновое уравнение, уравнение теплопроводности и стационарные уравнения, например, уравнение Лапласа.
1. Запишем волновое уравнение, описывающее свободные колебания струны

и, сравнив его с уравнением (13.2*), определим значения коэффициентов
А = - а 2; В = 0; С = 1,
вычислив выражение
В 2 – АС = 02 – (- а 2)×1 = а 2 > 0,
убедимся в том, что все волновые уравнения принадлежат к уравнениям ГТ.
2. Запишем уравнение теплопроводности, описывающее распределение нестационарного температурного поля в тонком стержне без влияния внешних источников температуры

и, сравнив его с уравнением (13.2*), определим значения коэффициентов
А = - а 2; В = 0; С = 0,
вычислив выражение
В 2 – АС = 02 – (- а 2)×0 =0,
убедимся в том, что все уравнения, описывающие тепловые и диффузионные процессы, принадлежат к уравнениям ПТ.
3. Запишем стационарное уравнение Лапласа, описывающее распределение нестационарного температурного поля в мембране без влияния внешних источников температуры
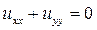
и, сравнив его с уравнением (13.2*), определим значения коэффициентов
А = 1; В = 0; С = 1,
вычислив выражение
В 2 – АС = 02 – 1×1 =-1< 0,
убедимся в том, что все стационарные уравнения принадлежат к уравнениям ЭТ.
Рассмотрим уравнение (13.1*) для того, чтобы проинтегрировать это уравнение необходимо по возможности привести его наиболее простому виду, то есть привести его к канонической форме.
Переход к канонической форме можно осуществить с помощью общих интегралов обыкновенного дифференциального уравнения второй степени
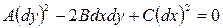 , (13.3)
, (13.3)
которое называется уравнением характеристик для уравнения (13.1*), а его интегралы характеристическими кривыми, или характеристиками.
Уравнение (13.3) можно, поделив на (dx)2, привести к виду
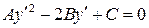 . (13.3*)
. (13.3*)
Это уравнение представляет собой уравнение первого порядка, второй степени, которое можно легко разрешить относительно производной
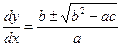 .
.
Полученное уравнение распадается на два уравнения
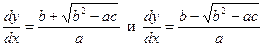 . (13.4)
. (13.4)
Решая эти уравнения, найдем два интеграла, т.е. два семейства характеристик:
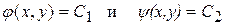 .
.
Используя эти интегралы, введем новые независимые переменные
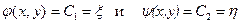 . (13.5)
. (13.5)
Вычислим все производные, входящие в уравнение (13.1*):
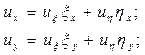
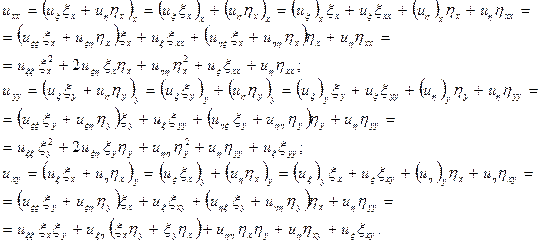 (13.6)
(13.6)
Подставляя вычисленные производные в уравнение (13.1*), получим его каноническую форму.
I. Для уравнений гиперболического типа уравнение характеристик имеет вид (13.3*), которое распадается на уравнения (13.4). С помощью их интегралов, произведя замену переменных (13.5) и, вычислив производные (13.6), после подстановки их в исходное уравнение, получим каноническую форму уравнения гиперболического типа
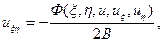 (13.7)
(13.7)
II. Для уравнений параболического типа уравнения характеристик принимает вид одного уравнения
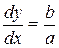 ,
,
которое имеет только одно семейство характеристик:
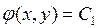 .
.
В этом случае для того, чтобы произвести замену переменных (13.5), необходимо в качестве недостающего второго интеграла C 2 выбрать некоторую произвольную функцию 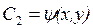 , такую, чтобы она была линейно независимая с функцией
, такую, чтобы она была линейно независимая с функцией 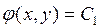 , т.е. для интегралов C 1 и C 2 должно выполнятся
, т.е. для интегралов C 1 и C 2 должно выполнятся
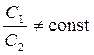 .
.
После такой замены, вычисления производных (13.6) и их подстановки в уравнение параболического типа получим его каноническую форму
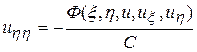 . (13.8)
. (13.8)
III. Для уравнений эллиптического типа уравнения характеристик принимает вид (13.3*) и оно распадается на два уравнения в комплексной форме:
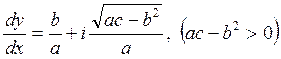 ,
,
и
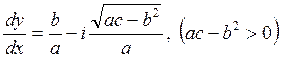 .
.
следовательно, уравнения (13) имеют два комплексно-сопряженных интеграла
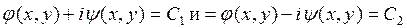 ,
,
причем функции 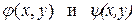 являются действительными функциями своих аргументов и с их помощью вводим новые переменные, причем
являются действительными функциями своих аргументов и с их помощью вводим новые переменные, причем
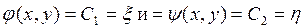 .
.
После такой замены, вычисления производных (13.6) и их подстановки в уравнение эллиптического типа получим его каноническую форму
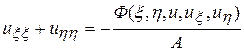 . (13.9)
. (13.9)
Пример 13.1. Привести к каноническому виду уравнение:
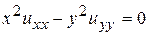 . (П13.1.1)
. (П13.1.1)
▲ Запишем общий вид уравнения второго порядка
 (П13. 1.2)
(П13. 1.2)
и сравним коэффициенты при производных в уравнении (П13.1. 2) и в исходном (П13.1. 1):
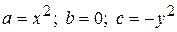 .
.
Определим, к какому типу принадлежит исходное уравнение:
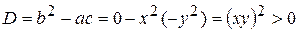 ,
,
следовательно, исходное уравнение (П13.1.1) принадлежит к уравнениям гиперболического типа.
Осуществим переход к канонической форме с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:
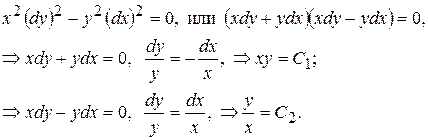
Следовательно, С 1 и С 2 определяют уравнения семейств характеристик. Тогда преобразование независимых переменных (13.5) будет иметь вид
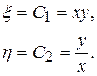
Найдем 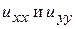 в новых переменных
в новых переменных
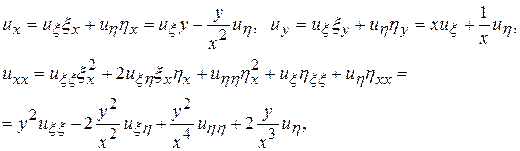
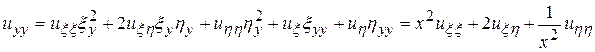 .Таким образом, исходное уравнение (П13.1. 1) в новых переменных имеет вид:
.Таким образом, исходное уравнение (П13.1. 1) в новых переменных имеет вид:

и после преобразований, получим
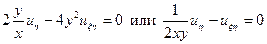 ,
,
с учетом того, что 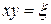 каноническая форма исходного уравнения имеет вид:
каноническая форма исходного уравнения имеет вид:
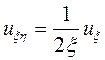 .▲
.▲
Пример 13.2. Привести к каноническому виду уравнение:
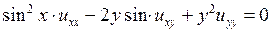 . (П13.2. 1)
. (П13.2. 1)
▲ Запишем общий вид уравнения второго порядка
 (П13.2.. 2)
(П13.2.. 2)
и сравним коэффициенты при производных в уравнении (П13.2. 2) и в исходном (П13.2.. 1):
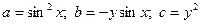 .
.
Определим, к какому типу принадлежит исходное уравнение (П13.2.1)
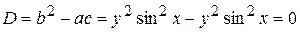 ,
,
следовательно, исходное уравнение (П13.2. 1) принадлежит к уравнениям параболического типа.
Осуществим переход к канонической форме с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:

Произведем замену переменных 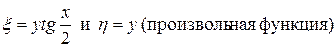 и вычислим
и вычислим 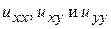 :
:
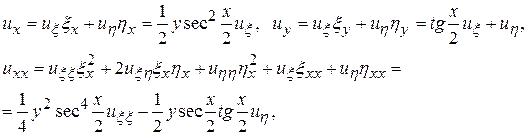
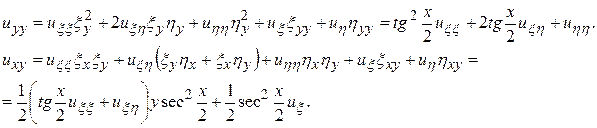
Подставим полученные производные в исходное уравнение (П13.2. 1) и после преобразований, получим

так как 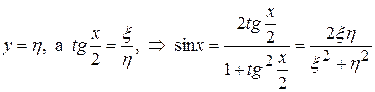 .
.
Таким образом, окончательно каноническая форма исходного уравнения (П13.2. 1) имеет вид:
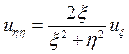 .▲
.▲
Пример 13.3. Привести к каноническому виду уравнение:
 .
.
▲ Запишем общий вид уравнения второго порядка

и сравним коэффициенты при производных в уравнении и в исходном:
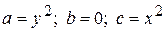 .
.
Определим, к какому типу принадлежит исходное уравнение
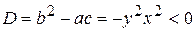 ,
,
следовательно, исходное уравнение принадлежит к уравнениям эллиптического типа.
Осуществим переход к канонической форме с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:
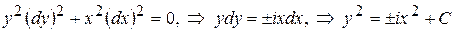 .
.
Следовательно, получаем два семейства мнимых характеристик
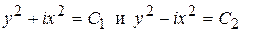 .
.
Произведем замену 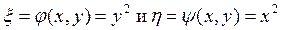
и вычислим 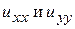 :
:
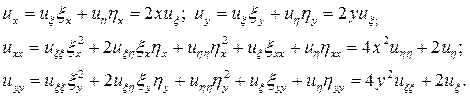
Подставим полученные производные в исходное уравнение и после преобразований окончательно получим каноническую форму исходного уравнения

или
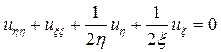 .▲
.▲
Пример 13.4. Найти решение уравнения
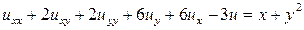 ,
,
▲ Во-первых, осуществим переход к канонической форме с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:
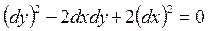 или
или 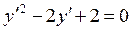 .
.
Это степенное уравнение первого порядка распадается на два уравнения
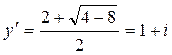 и
и 
Следовательно, получаем два семейства мнимых характеристик
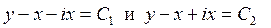 .
.
Произведем замену 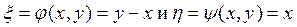
и вычислим 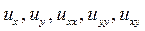 :
:

Подставим полученные производные в исходное уравнение и после преобразований

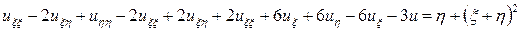
окончательно получим каноническую форму исходного уравнения
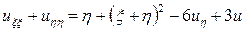 .▲
.▲
Приведение исходного уравнения к канонической форме в ряде случаев позволяет достаточно легко найти общее решение исходного уравнения. Поскольку в данном методе используется уравнение характеристик (13.3), то данным метод нахождения общего решения называется методом характеристик. Рассмотрим примеры нахождения решения уравнений методом характеристик.
Пример 13.5. Найти общее решение уравнения:
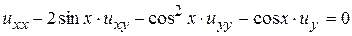 .
.
▲ Запишем общий вид уравнения второго порядка

и сравним коэффициенты при производных в этом уравнении и в исходном:

Осуществим переход к канонической форме с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:
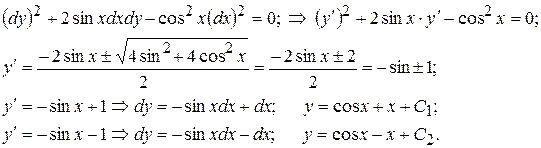
Следовательно, С 1 и С 2 определяют уравнения семейств характеристик. Тогда преобразование независимых переменных (13.5) будет иметь вид
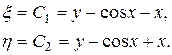
Найдем 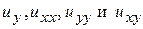 в новых переменных
в новых переменных

Подставим полученные производные в исходное уравнение, и после преобразований окончательно получим каноническую форму исходного уравнения
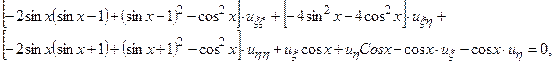
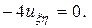 или
или 
Интегрируя дважды это уравнение, получим решение

Возвращаясь к «старым» переменным х и у, запишем окончательно общее решение исходного уравнения
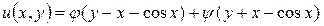 .▲
.▲
Пример 13.6. Найти решение уравнения
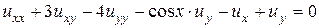 ,
,
▲ Во-первых, осуществим переход к канонической форме с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:
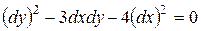 ,
,
которое распадается на два уравнения
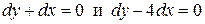 ,
,
для которых семейство характеристик имеет вид
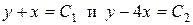 .
.
Заменой переменных

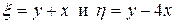 ,
,
приведем исходное уравнение к каноническому виду.
Вычислим 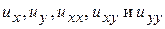 :
:
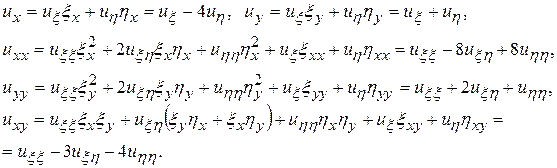
Подставим полученные производные в исходное уравнение и после преобразований получим каноническую форму исходного уравнения
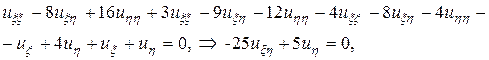
или
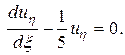 (П13.6.1)
(П13.6.1)
Сделаем замену
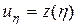 , (П13.6.2)
, (П13.6.2)
тогда уравнение (П13.6.1) принимает вид
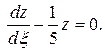
Это однородное линейное уравнение, которое к тому же является уравнением с разделяющимися переменными. Разделив переменные, найдем 
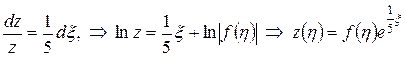 .
.
Подставив найденную функцию  в (П13.6.2) и проинтегрировав полученное выражение, окончательно получим решение уравнения (П13.6.1)
в (П13.6.2) и проинтегрировав полученное выражение, окончательно получим решение уравнения (П13.6.1)
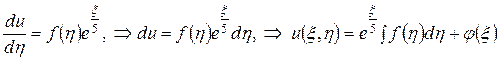 .
.
Обозначив 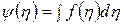 , получим
, получим
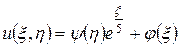
и, возвращаясь к «старым» переменным получим общее решение исходного уравнения
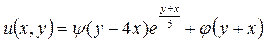 .▲
.▲
Пример 13.7. Найти решение уравнения
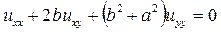 ,
,
▲ Во-первых, осуществим переход к канонической форме с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:
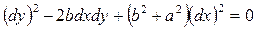 ,
,
которое распадается на два уравнения
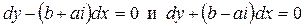 ,
,
для которых семейство характеристик имеет вид
 .
.
Заменой переменных

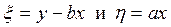 ,
,
приведем исходное уравнение к каноническому виду.
Вычислим 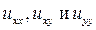 :
:
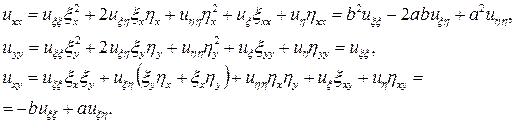
Подставим полученные производные в исходное уравнение и после преобразований получим каноническую форму исходного уравнения


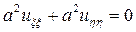 ,
,
если а ≠ 0, то окончательный вид канонической формы исходного уравнения будет выглядеть следующим образом
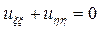 . (П13.7.1)
. (П13.7.1)
Уравнение (П13.7.1) означает, что функция u (ξ, η) является вещественной (или мнимой) частью аналитической функции f (ξ + ηi). Поэтому общее решение исходного уравнения имеет вид
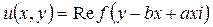 .▲
.▲
Пример 13.8. Найти решение уравнения
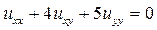 ,
,
▲ Во-первых, осуществим переход к канонической форме с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:
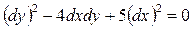 ,
,
которое распадается на два уравнения
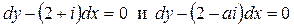 ,
,
для которых семейство характеристик имеет вид
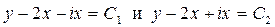 .
.
Заменой переменных

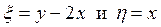 ,
,
приведем исходное уравнение к каноническому виду.
Вычислим 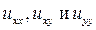 :
:

Подставим полученные производные в исходное уравнение и после преобразований получим каноническую форму исходного уравнения
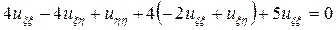

окончательный вид канонической формы исходного уравнения будет выглядеть следующим образом
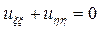 . (П13.8.1)
. (П13.8.1)
Уравнение (П13.8.1) означает, что функция u (ξ, η) является вещественной (или мнимой) частью аналитической функции f (ξ + ηi). Поэтому общее решение исходного уравнения имеет вид
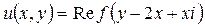 .▲
.▲
Определить тип уравнения и привести к каноническому виду
13.1. 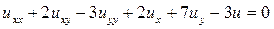 .
.
13.2. 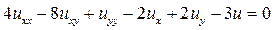 .
.
13.3. 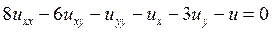 .
.
13.4. 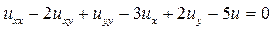 .
.
13.5. 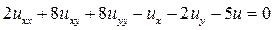 .
.
13.6. 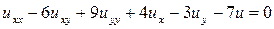 .
.
13.7. 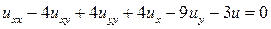 .
.
13.8. 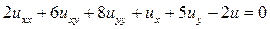 .
.
13.9. 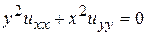 .
.
13.10. 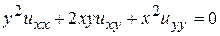 .
.
Найти общее решение уравнений
13.11. 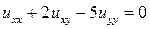 . 13.12.
. 13.12. 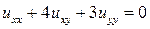 .
.
13.13. 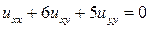 . 13.14.
. 13.14. 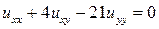 .
.
13.15. 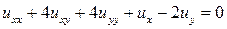 .
.
13.16. 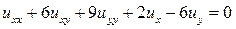 .
.
13.17. 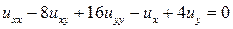 .
.
13.18. 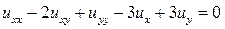 .
.
13.19. 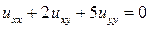 . 13.20.
. 13.20. 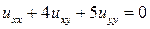 .
.
13.21. 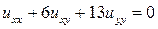 . 13.22.
. 13.22. 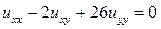 .
.
 2014-02-12
2014-02-12 2115
2115








