Рассмотрим задачу об определении малых продольных колебаний упругого прямолинейного однородного стержня длиной l при t >0, считая, что во время движения поперечные сечения остаются параллельными плоскости перпендикулярной к оси стержня.
Рассмотрим рисунок, на котором изображен такой стержень.
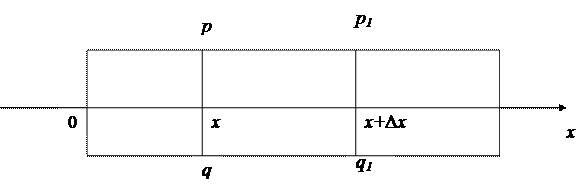 |
Рис.12.1
Пусть ось х совпадает с направлением оси стержня и пусть х – координата сечения pq, когда оно находится в покое. Поскольку мы изучаем малые продольные колебания стержня, то это значит, что внешние силы и силы инерции можно считать направленными вдоль оси стержня. Обозначим через u(x,t) смещение этого сечения в момент t. В рамках нашего предположения о том, что во время движения поперечные сечения остаются параллельными плоскости перпендикулярной к оси стержня, смещения в точке х+∆х будет
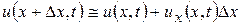 .
.
Поэтому относительное удлинение стержня в сечении х будет равно ux (x,t). По закону Гука натяжение в этом сечении равно
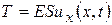 ,
,
где S – площадь поперечного сечения, Е – модуль упругости материала стержня.
Уравнение колебаний стержня получим, если приравняем нулю сумму всех сил, включая силы инерции, действующие на участок pq,p 1 q 1. Равнодействующая сила равна
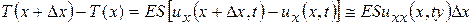 .
.
Пусть p (x,t) – объемная плотность внешних сил. Тогда на участок pq,p 1 q 1 действует внешняя сила S p (x,t)∆ x и сила инерции  . Сумма всех сил по принципу Даламбера равна нулю, т.е.
. Сумма всех сил по принципу Даламбера равна нулю, т.е.
 . (12.6)
. (12.6)
Отсюда находим
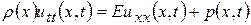 , (12.7)
, (12.7)
кроме того, функция u (x,t) удовлетворяет начальным условиям
 ,
,
где  - заданные функции. Если
- заданные функции. Если  (стержень однородный), то уравнение (12.7) принимает вид
(стержень однородный), то уравнение (12.7) принимает вид
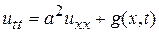 , (12.8)
, (12.8)
где  .
.
Таким образом, мы видим, что волновое уравнение (12.8) также описывает и малые продольные колебания стержня.
 2014-02-12
2014-02-12 1161
1161
