2014-02-12
498
Лекция 12. ОСНОВНЫЕ ВИДЫ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Задания для самостоятельной работы
Найти общий интеграл уравнений
11.1.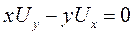 
. 11.2. 
.
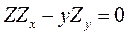11.3.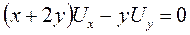 
11.4.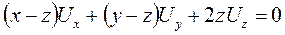 
. 11.5. 
.
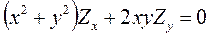11.6.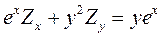 
. 11.7. 
.
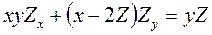11.8.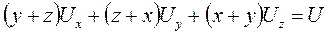 
.
11.9.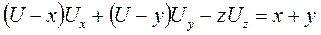 
.
Найти решения уравнений, удовлетворяющие начальным условиям
11.10.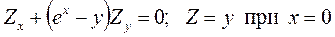 
.
11.11.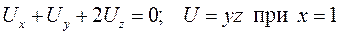 
.
11.12.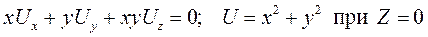 
.
11.13.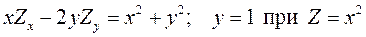 
.
11.14.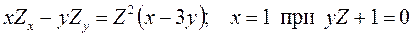 
.
11.15.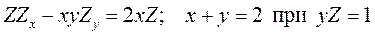 
.
Рассмотрим струну, под которой понимается тонкая нить, не сопротивляющаяся изгибу, длиной l. Пусть эта струна в плоскости (x,u) совершает малые поперечные колебания около своего положения равновесия, совпадающего с осью Ох, то есть все точки струны движутся перпендикулярно оси Ох. Обозначим через u(x,t) отклонение от положения равновесия точки струны с абсциссой х в момент времени t. Так как струна не сопротивляется изгибу, то ее натяжение 
в точке х в момент времени t направлено по касательной к струне в точке х. Любой участок струны (а,b) после отклонения от положения равновесия в предположении о пренебрежении величинами высшего порядка малости по сравнению с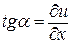 
, не изменит своей длины
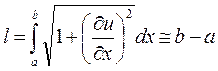(12.1)
и, следовательно, величина натяжения 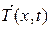будет постоянной Т 0, не зависящей от х и t, так как закон Гука гласит: изменение натяжения пропорционально изменению длины выделенного участка.
Составим уравнение движения струны. На элемент струны (х, х+ Δ х) действуют силы натяжения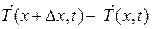 
и внешняя сила 
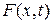, действующая на струну в точке х в момент времени t и направленная перпендикулярно оси Ох.
Сумма сил, действующих на струну, согласно закону Ньютона должна быть равна произведению массы элемента струны на его ускорение
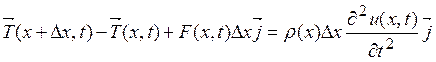, (12.2)
где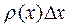 
- масса элемента струны (х, х+ Δ х); 
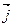- единичный вектор, направленный вдоль оси u.
Проектируя векторное равенство (12.2) на ось u, получим
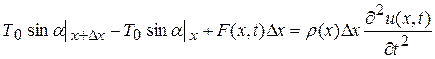, (12.3)
но в рамках приближения
,
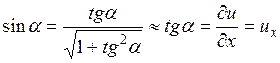поэтому выражение (12.3) принимает вид
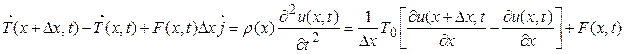и при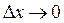 
, получим
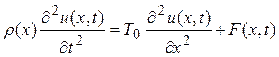. (12.4)
Это и есть уравнение малых поперечных колебаний струны. Если F(x,t)¹ 0, то колебания струны будут вынужденными, а если F(x,t)= 0, то колебания струны будут свободными.
Если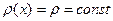 
, то уравнение (12.4) принимает вид
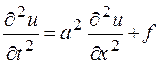, (12.5)
где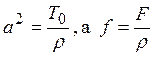 
.
Уравнение (12.5) называется одномерным волновым уравнением.
