Лекция 15. РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ
Поставим задачу Коши для однородного волнового уравнения, описывающего свободные колебания однородной струны, т.е. найдем решение уравнения
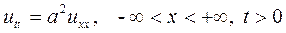 , (15.1)
, (15.1)
удовлетворяющее начальным условиям
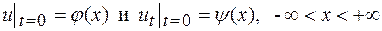 . (15.2)
. (15.2)
Эту задачу (15.1), (15.2) можно решить методом Даламбера.
Осуществим переход к канонической форме уравнения (15.1) с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:
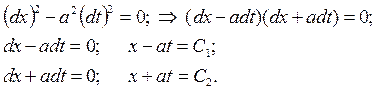
Следовательно, С 1 и С 2 определяют уравнения семейств характеристик. Тогда преобразование независимых переменных (13.5) будет иметь вид
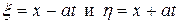 .
.
Вычислим 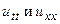 в новых переменных:
в новых переменных:
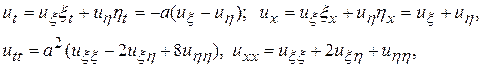
и подставим их в уравнение (15.1)
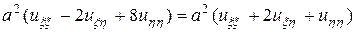 .
.
После сокращений получим
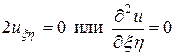 . (15.3)
. (15.3)
Интегрирование этого уравнения дает
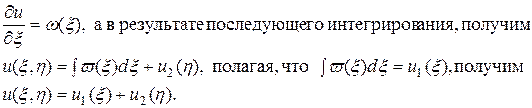
Возвращаясь к переменным х и у, окончательно будем иметь
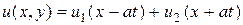 . (15.4)
. (15.4)
Функция 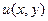 является решением уравнения (15.1), если и 1 и и 2 - произвольные дважды дифференцируемые функции. В решении (15.4) необходимо выбрать функции и 1 и и 2 так, чтобы удовлетворить начальным условиям (15.2)
является решением уравнения (15.1), если и 1 и и 2 - произвольные дважды дифференцируемые функции. В решении (15.4) необходимо выбрать функции и 1 и и 2 так, чтобы удовлетворить начальным условиям (15.2)
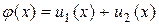 (15.5)
(15.5)
и
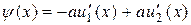 (15.6)
(15.6)
Проинтегрировав уравнение (15.6) в пределах от х 0 до х, получим
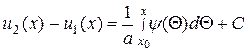 . (15.7)
. (15.7)
Разрешив совместно уравнения (15.5) и (15.7) относительно и 1(х) и и 2(х), получим
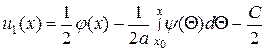 (15.8)
(15.8)
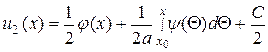 (15.9)
(15.9)
Подставив (15.8) и (15.9) в решение (15.4) окончательно получим решение задачи Коши для однородного волнового уравнения
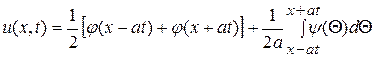 . (15.10)
. (15.10)
Формула (15.10) называется формулой Даламбера для однородного волнового уравнения, описывающего свободные колебания однородной струны. Эта формула дает классическое решение задачи (15.1) - (15.2) только в предположении, что функция 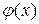 имеет производные до второго порядка включительно, а функция
имеет производные до второго порядка включительно, а функция 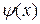 - до первого.
- до первого.
Решение задачи Коши неоднородного волнового уравнения, описывающего вынужденные колебания однородной струны
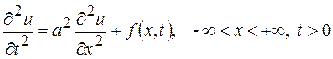 , (15.11)
, (15.11)
удовлетворяющего начальным условиям
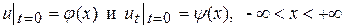 , (15.12)
, (15.12)
можно получить по формуле
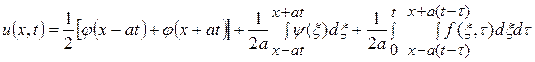 (15.13)
(15.13)
Это формула Даламбера, дающая решение задачи Коши для неоднородного волнового уравнения, описывающего вынужденные колебания однородной струны.
Пример 15.1. Найти решение уравнения
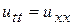 ,
,
удовлетворяющее начальным условиям
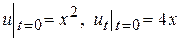 .
.
? Для нахождения решения исходной задачи Коши используем формулу Даламбера (15.10)
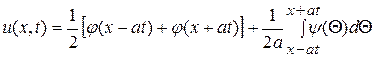 ,
,
в которой 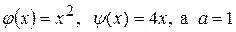 .
.
Следовательно,
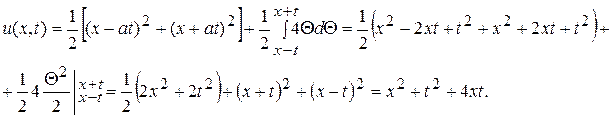 Окончательно решение исходной задачи имеет вид
Окончательно решение исходной задачи имеет вид
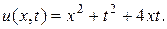 ?
?
Пример 15.2. Найти решение уравнения
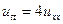 ,
,
удовлетворяющее начальным условиям
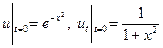 .
.
? Для нахождения решения исходной задачи Коши используем формулу Даламбера (15.10)
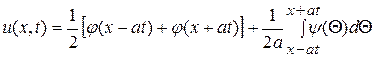 ,
,
в которой 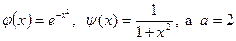 .
.
Следовательно,
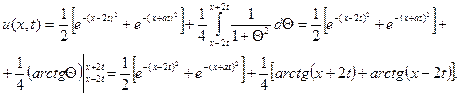
Окончательно решение исходной задачи имеет вид
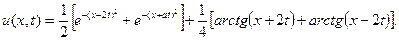 ?
?
Пример 15.3. Найти решение уравнения
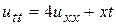 ,
,
удовлетворяющее начальным условиям
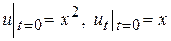 .
.
? Для нахождения решения исходной задачи Коши используем формулу Даламбера (15.13)
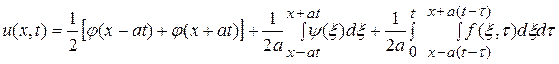 в которой
в которой 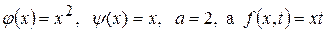 .
.
Следовательно,
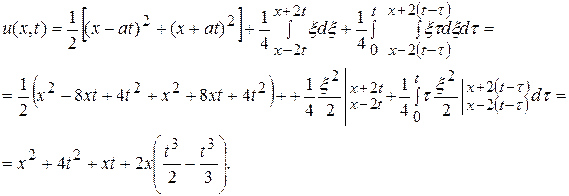 Окончательно решение исходной задачи имеет вид
Окончательно решение исходной задачи имеет вид
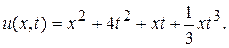 ?
?
 2014-02-12
2014-02-12 18640
18640








