Задача Коши для волнового уравнения, описывающего вынужденные колебания какого-либо трехмерного объекта
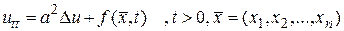 (15.14)
(15.14)
с начальными условиями
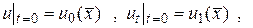 (15.15)
(15.15)
где 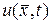 – неизвестная функция;
– неизвестная функция; 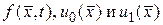 – заданные функции;
– заданные функции; 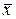 - вектор с координатами (x, y, z), может быть решена методом Тейлора. Суть метода заключается в том, что решение поставленной задачи ищется в виде ряда
- вектор с координатами (x, y, z), может быть решена методом Тейлора. Суть метода заключается в том, что решение поставленной задачи ищется в виде ряда
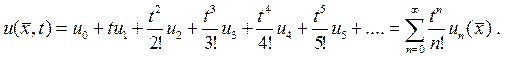
 (15.16)
(15.16)
Если найти все функции 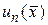 , то по формуле (15.16) получим решение исходной задачи Коши. Заметим, что
, то по формуле (15.16) получим решение исходной задачи Коши. Заметим, что 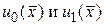 определяются из начальных условий (15.15), остальные коэффициенты
определяются из начальных условий (15.15), остальные коэффициенты 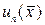 можно найти по формуле
можно найти по формуле
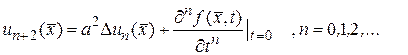 (15.17)
(15.17)
Пример 15.4. Найти решение уравнения
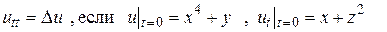
▲ Здесь 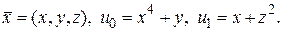
Так как 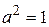 и
и 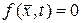 , то по (15.17)
, то по (15.17) 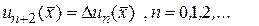
Отсюда, при n = 0, получим
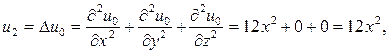
при n = 1, получим
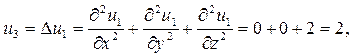
при n = 2, получим
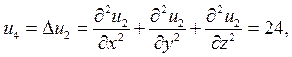
при n = 3, получим
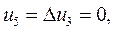
при n = 4, получим
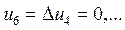
то есть, все остальные 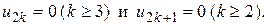
Подставляем найденные 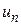 в решение (15.16)
в решение (15.16)
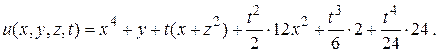
Окончательно,
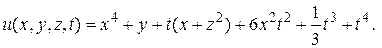 ▲
▲
Пример 15.5. Найти решение уравнения
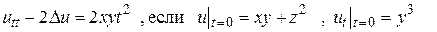
▲ Здесь 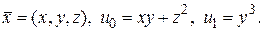 Так как
Так как 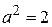 и
и 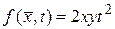 , то по (15.17)
, то по (15.17)
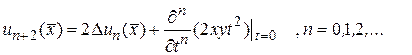
Найдем 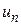 по этой формуле
по этой формуле
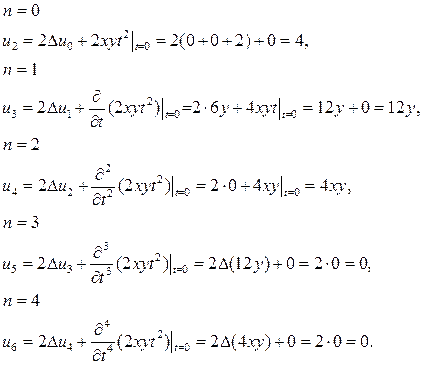
И так далее, все остальные 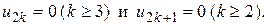
Подставляем полученные 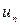 в решение (15.16)
в решение (15.16)
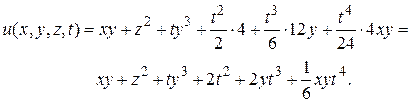
Таким образом, решением исходного уравнения является функция
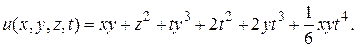 ▲
▲
 2014-02-12
2014-02-12 2466
2466
