Формула Дирихле. Пусть 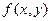 непрерывна в треугольнике
непрерывна в треугольнике 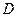 :
: 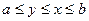 (рис. 21.1).
(рис. 21.1).
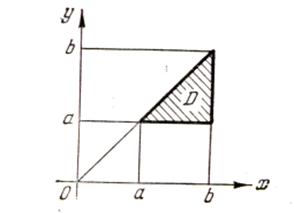
Рис. 21.1
Преобразуя двойной интеграл 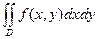 двумя способами в двукратный и сравнивая результаты, получим искомую формулу Дирихле:
двумя способами в двукратный и сравнивая результаты, получим искомую формулу Дирихле:
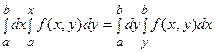 (21.3)
(21.3)
Свертка функций. Пусть  и
и 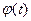 — непрерывные, комплекснозначные функции на
— непрерывные, комплекснозначные функции на 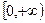 . Сверткой функций
. Сверткой функций и
и 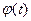 называется функция, обозначаемая
называется функция, обозначаемая 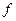 *
*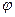 и определяемая равенством
и определяемая равенством
(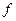 *
*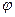 )
)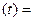
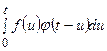 .
.
Это будет непрерывная функция на 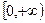 . Очевидно,
. Очевидно,
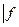 *
*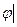
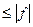 *
*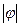
при 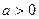 с помощью формулы Дирихле находим:
с помощью формулы Дирихле находим:
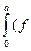 *
*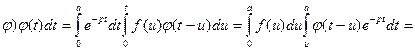
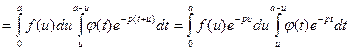 ;
;
следовательно, если записать внутренний интеграл
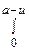 в виде
в виде 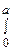 -
-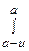 , получим формулу
, получим формулу
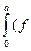 *
*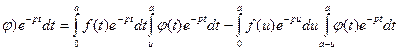 (21.4)
(21.4)
Из (21.4) следует, что при 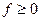 и
и 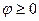 и действительном
и действительном 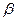
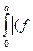 *
*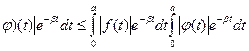 ,
,
откуда видно, что если 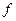 и
и 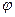 оригиналы, то
оригиналы, то 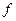 *
*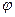 — тоже оригинал, причем показатель роста
— тоже оригинал, причем показатель роста 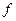 *
*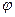 не более наибольшего из показателей роста
не более наибольшего из показателей роста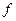 и
и 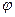 .
.
 2014-02-12
2014-02-12 618
618








