Лекция 21. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Часть 3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ПРИМЕНЕНИЕ ПРИ РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Преобразование Лапласа это такое преобразование, которое ставит в соответствие комплекснозначной функции  действительного переменного
действительного переменного 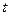 некоторую функцию
некоторую функцию  комплексного переменного
комплексного переменного 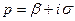 с помощью следующего соотношения
с помощью следующего соотношения
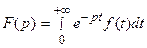 . (21.1)
. (21.1)
Интеграл, стоящий в правой части, называют интегралом Лапласа функции  . При этом эта функция должна удовлетворять следующим условиям:
. При этом эта функция должна удовлетворять следующим условиям:
1.  задана на множестве действительных чисел (на числовой прямой) R, причем для всех
задана на множестве действительных чисел (на числовой прямой) R, причем для всех 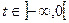 функция
функция 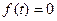 ;
;
2. при 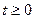 функция
функция  на любом ограниченном промежутке имеет не более чем конечное число точек разрыва первого рода;
на любом ограниченном промежутке имеет не более чем конечное число точек разрыва первого рода;
3. существуют такие числа 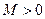 и
и 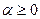 , что для всех
, что для всех 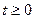 функция
функция  является ограниченной -
является ограниченной - 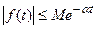 , причем точная нижняя граница числа
, причем точная нижняя граница числа 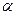 равна числу
равна числу 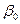 (
(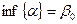 ), которое называется показателем степени роста функции
), которое называется показателем степени роста функции  , следовательно, можно констатировать, что функция
, следовательно, можно констатировать, что функция  в данном случае имеет ограниченный рост.
в данном случае имеет ограниченный рост.
Если функция  имеет ограниченный рост, то
имеет ограниченный рост, то 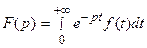 является аналитической функцией комплексного переменного
является аналитической функцией комплексного переменного 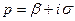 в полуплоскости Re
в полуплоскости Re 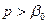 , где
, где 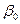 - показатель степени роста функции
- показатель степени роста функции  , который еще называют абсциссой абсолютной сходимости интеграла Лапласа
, который еще называют абсциссой абсолютной сходимости интеграла Лапласа 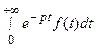 .
.
Резюмируя сказанное можно утверждать:
- комплекснозначная функция  , непрерывная на интервале
, непрерывная на интервале 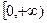 , за исключением изолированных точек*, и имеющая ограниченный рост, называется оригиналом;
, за исключением изолированных точек*, и имеющая ограниченный рост, называется оригиналом;
- аналитическая функция  комплексного переменного
комплексного переменного 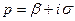 , определенная формулой (21.1) при Re
, определенная формулой (21.1) при Re 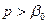 , называется изображением оригинала
, называется изображением оригинала  .
.
Преобразование Лапласа (21.1) схематично можно записать в виде
 ≒
≒ .
.
Употребляется также обозначение вида
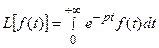 ,
,
где 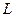 - знак преобразования Лапласа.
- знак преобразования Лапласа.
Замечания.
1. Если функция  является оригиналом, то и
является оригиналом, то и 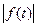 также будет оригиналом с тем же показателем роста.
также будет оригиналом с тем же показателем роста.
2. Если функции 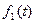 ,
, 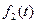 ,…,
,…,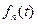 , являются оригиналами, то их линейная комбинация также будет оригиналом. Если функция
, являются оригиналами, то их линейная комбинация также будет оригиналом. Если функция  является оригиналом, то функции
является оригиналом, то функции 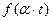 (
(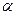 - положительное число),
- положительное число), 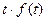 ,
, 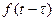 (
(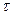 – действительное число),
– действительное число), 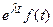 (
(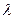 - комплексное число) тоже будут оригиналами.
- комплексное число) тоже будут оригиналами.
3. Можно утверждать, что если комплекснозначная функция  является оригиналом, то функция
является оригиналом, то функция 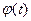 , определяемая выражением
, определяемая выражением
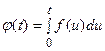
будет непрерывным на интервале 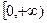 оригиналом.
оригиналом.
Непрерывность функции 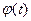 следует из абсолютной интегрируемости функции
следует из абсолютной интегрируемости функции  на каждом сегменте
на каждом сегменте 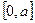 , где
, где 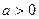 . Далее, если
. Далее, если 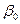 – показатель степени роста функции
– показатель степени роста функции  , а
, а 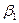 – положительное число больше
– положительное число больше 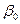 , причем
, причем 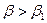 (
(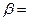 Re
Re 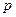 ), то в случае, когда
), то в случае, когда 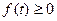 имеем:
имеем:
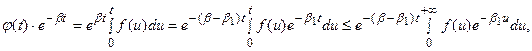
откуда следует, что интеграл 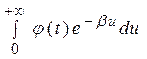 сходится, а функция
сходится, а функция 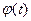 является оригиналом.
является оригиналом.
4. Если функция  комплексного переменного
комплексного переменного 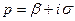 , определенная формулой (21.1) является изображением, то при Re
, определенная формулой (21.1) является изображением, то при Re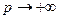 следует, что
следует, что 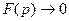 .
.
 2014-02-12
2014-02-12 841
841








