1. Однородность. Если  ≒
≒ , то
, то 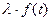 ≒
≒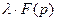 (
(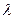 - любое комплексное число).
- любое комплексное число).
Действительно,
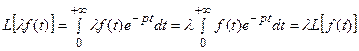 .
.
Следовательно, 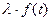 ≒
≒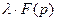 .
.
2. Аддитивность. Если  ≒
≒ и
и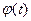 ≒
≒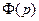 , то
, то
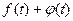 ≒
≒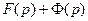 .
.
Действительно,
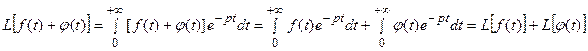 .
.
Следовательно, 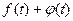 ≒
≒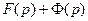 .
.
3. Подобие. Если  ≒
≒ , то
, то 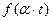 ≒
≒ 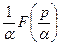 .
.
Действительно,
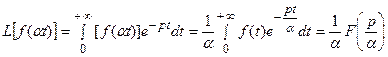 .
.
Следовательно, 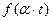 ≒
≒ 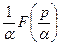 .
.
4. Дифференцирование оригинала. Если функция  непрерывно дифференцируема на интервале
непрерывно дифференцируема на интервале 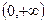 является оригиналом и существует конечный предел -
является оригиналом и существует конечный предел -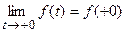 , а также, если
, а также, если 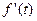 есть то же оригинал, то из
есть то же оригинал, то из  ≒
≒ следует:
следует:
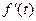 ≒
≒ 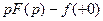 .
.
Действительно, интегрирование по частям дает при 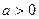
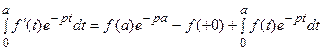 .
.
Если Re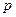 больше показателей роста функции
больше показателей роста функции  и ее производной
и ее производной 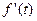 , то оба интеграла стремятся к конечным пределам при
, то оба интеграла стремятся к конечным пределам при 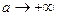 , следовательно, с учетом того, что интеграл вида
, следовательно, с учетом того, что интеграл вида 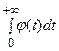 не может абсолютно сходиться, если функция
не может абсолютно сходиться, если функция 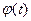 при
при 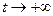 стремится к пределу, отличному от нуля,
стремится к пределу, отличному от нуля, 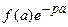 стремится к конечному пределу, но этот предел не может быть отличен от нуля. Следовательно, в пределе при
стремится к конечному пределу, но этот предел не может быть отличен от нуля. Следовательно, в пределе при 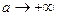 получим
получим
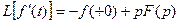 .
.
4.1. Обобщение. Если функция 
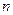 разнепрерывно дифференцируема на интервале
разнепрерывно дифференцируема на интервале 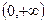 является оригиналом и все ее производные до
является оригиналом и все ее производные до 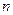 -го порядкавключительно –
-го порядкавключительно – 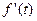 ,
, 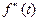 ,…,
,…, 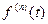 , то же есть оригиналы, а также существуют конечные пределы -
, то же есть оригиналы, а также существуют конечные пределы -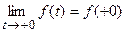 ,
, 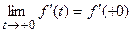 ,
, 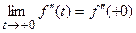 ,…,
,…,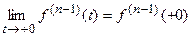 , то из
, то из  ≒
≒ следует:
следует:
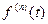 ≒
≒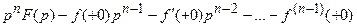 .
.
Для доказательства существования изображения производной 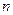 -го порядка используется свойство 4 по индукции.
-го порядка используется свойство 4 по индукции.
5. Дифференцирование изображения. Если  ≒
≒ , то
, то
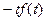 ≒
≒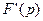 .
.
Действительно,
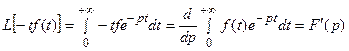
Следовательно, 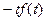 ≒
≒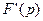 .
.
5.1. Обобщение. Если  ≒
≒ , то
, то 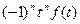 ≒
≒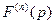 .
.
Для доказательства этого утверждения используется метод индукции по свойству 5.
6. Интегрирование оригинала. Если функция  являющаяся оригиналом, непрерывна на интервале
являющаяся оригиналом, непрерывна на интервале 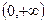 и имеет изображение
и имеет изображение  , то
, то
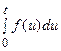 ≒
≒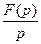 .
.
Действительно, если функция 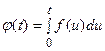 является оригиналом, которому соответствует изображение
является оригиналом, которому соответствует изображение 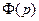 , т.е.
, т.е. 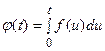 ≒
≒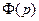 , тогда
, тогда 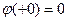 и по свойству 4 следует, что
и по свойству 4 следует, что  ≒
≒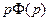 , следовательно,
, следовательно,
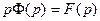 или
или 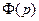 =
=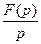 .
.
7. Интегрирование изображения. Если функция  является оригиналом, а также является оригиналом
является оригиналом, а также является оригиналом 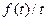 , то из
, то из  ≒
≒ следует:
следует:
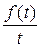 ≒
≒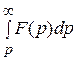
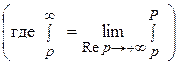 .
.
Действительно, если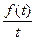 ≒
≒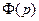 , тогда по свойству 5
, тогда по свойству 5 ≒
≒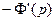 , следовательно,
, следовательно, 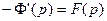 . Интегрируя полученное равенство в пределах от
. Интегрируя полученное равенство в пределах от 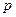 до
до 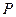 , найдем:
, найдем:
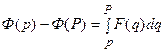 ,
,
следовательно, с учетом того, что Re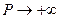 следует, что
следует, что 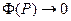 , получим:
, получим:
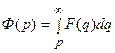 .
.
8. Запаздывание. Если  ≒
≒ , то
, то 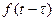 ≒
≒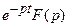 (
(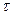 – любое положительное число).
– любое положительное число).
Действительно,
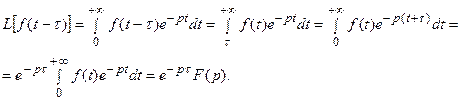
9. Умножение оригинала на показательную функцию (смещение изображения). Если  ≒
≒ , то
, то 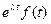 ≒
≒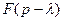 (
(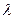 - любое комплексное число).
- любое комплексное число).
Действительно,
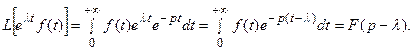
 2014-02-12
2014-02-12 464
464








