Лекция 20. Закономерности преломления и отражения плоских упругих волн на плоскости контакта твердых тел

Рассмотрим конкретный пример.

Пусть в воздухе при а = 330 м/с и ρ = 1,26 кг/м³ распростра­няется упругая волна V -V₀ = Δ V = 1 м/с. В этой волне амплиту­да давления составляет Δ p = 1,26·330·1 = 4,05·10² Па.

При ударно-вращательном, ударно-поворотном и вращательно-ударном способах бурения взрывных скважин и шпу­ров одним из основных режимных параметров, определяющих эффективность этих способов бурения, является величина энер­гии удара А, под действием которой зубья бурового инстру­мента внедряются в породу на заданную глубину h_в, разрушая её.

Удар поршня-ударника по штанге или по инструменту гене­рирует в последних импульс напряжений, скорость частиц ме­талла с в котором обычно не превышает 8 м/с. При скорости распространения импульсов напряжений с ~ 5000 м/с, процессы их распространения и преломления в соударяющихся элементах достаточно точно описываются одномерной волновой теорией Сен-Венана для плоских упругих волн малой амплитуды.

При взрыве заряда промышленных взрывчатых ве5ществ (ПВВ) в зоне нерегулируемого дробления, то есть при r ≥ b ₀, где b ₀— радиус зоны регулируемого дробле­ния, обычно не превышающий 5 м, скорость частиц во взрывной волне не превышает 2 м/с. И в этом случае распространение и преломление взрывных волн, распространяющихся по отдельностям, тоже достаточно надежно описывается теорией Сен-Венана.

Для определенности рассмотрим процессы преломления и отражения упругих волн малой амплитуды при ударном контак­те двух отдельностей горной породы под действием взрывных волн. Для случая же соударения двух элементов буровых машин установленные ниже закономерности могут быть использованы практически без изменений, только в них слово «отдельность» должно быть заменено на слова «буровая штанга», «поршень-ударник», «буровой инструмент» и т. п.

Итак, рассматриваются по Сен-Венану процессы распро­странения и преломления плоских упругих волн напряжений малой амплитуды в длинных отдельностях. При этом под длин­ными отдельностями понимаются такие, для которых попереч­ные размеры существенно меньше продольных. В этом случае движением частиц в направлениях, перпендикулярных к оси отдельностей, можно пренебречь.

Направим ось X по оси отдельности, поместив начало коор­динат в произвольную точку 0 этой отдельности (рис. 20.1).

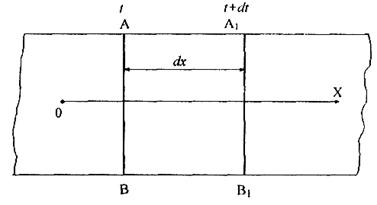
Рис. 20.1. Схема распространения плоской упругой волны малой амплитуды

Предположим, что по отдельности распространяется упру­гая волна, двигающаяся слева направо. Пусть в некоторый мо­мент времени t фронт волны находится в сечении АВ. Так что перед фронтом волны справа от сечения АВ частицы породы находятся в покое, а слева от АВ — в движении, такую поверх­ность принято называть поверхностью разрыва. Продольное перемещение частиц породы обозначим буквой U, скорость частиц— v, напряжение — σ, деформацию — ε. В каждой точке попе­речного сечения отдельности в любой момент времени все ука­занные величины одинаковы, т.е. имеет место распространение плоских волн по отдельности, а указанные параметры являются функциями только двух переменных х и t.

В рассматриваемый момент времени t на фронте АВ пере­мещение частиц U(x,t) = 0. За время dt этот фронт, двигаясь с некоторой скоростью с, переместится на расстояние dx = сdt в положение А ₁ В ₁. Причем и в этом новом положении для поверх­ности разрыва имеет место равенство

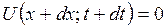
Разлагая функции U в ряд Тейлора и ограничиваясь членами первого порядка малости по dt и dx, получаем

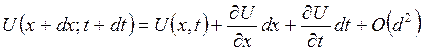(20.1)

где O(d²) — члены второго и более высоких порядков малости по dx и dt.

Поскольку

,

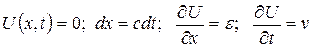то из (20.1) получается следующее соотношение:

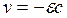(20.2)

Соотношение (20.2) — частный случай кинематических условий на поверхности разрыва. В случае, если волна напряже­ний распространяется по уже возмущенным частицам отдельно­сти, имеющим скорость v ₁ напряжение σ ₁, деформацию ε ₁, а во фронте волны соответствующие величины имеют значения v ₂, σ ₂, ε ₂, то вместо (20.2) получается соотношение

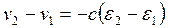(20.3)

В случае непрерывного распределения возмущений вдоль продольной оси отдельности соотношение (20.3) может быть представлено в дифференциальной форме:

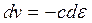(20.4)

Рассмотрим теперь динамическое условие на поверхности разрыва АВ.

За время dt частицы, заключенные между сечениями АВ и А ₁ В ₁, перешли из состояния покоя в состояние движения со ско­ростью v. Это произошло за счет продольного напряжения σ, действующего в сечении АВ. Если ρ — плотность материала от­дельности, S — площадь ее поперечного сечения, то масса, пе­решедшая за время dt из состояния покоя в состояние движения, равна Scρdt, так что теорема об изменении количества движения частиц в объеме ВА А ₁ В ₁, запишется в виде

,

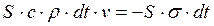где в правой части записан импульс силы, действующей на эти частицы. При этом учтено, что распространяющийся вправо им­пульс напряжений является импульсом сжатия, а величина на­пряжения в нем отрицательна. После сокращения на S и dt получим

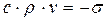(20.5)

При распространении импульса напряжения по уже возму­щенным частицам отдельности вместо (20.5) имеет место со­отношение

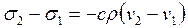(20.6)

В случае же непрерывного распределения возмущений в импульсе напряжений получается соотношение

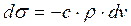(20.7)

Исключая dv из (20.4) и (20.7), для скорости распростра­нения импульса напряжений, получаем

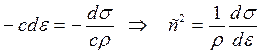(20.8)

В случае распространения в отдельности упругих напряже­ний малой амплитуды производная 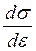равна Е, так что для скорости распространения упругих волн напряжений в отдель­ности получается

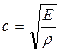(20.9)

Выведем теперь дифференциальное уравнение распростра­нения в отдельности упругих возмущений малой амплитуды. Рассмотрим слой толщиною dx в зоне возмущения (см. рис. 20.1). На этот слой слева (сечение АВ)действует напряжение σ, а справа (сечение А ₁ В ₁)— напряжение σ + dσ.

Рассмотрим случай отдельности постоянного поперечного сечения. Пусть на частицы слоя действует массовая сила Q, плотность которой 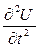есть ускорение частиц. Тогда полная величина массовой силы, действующей на слой отдельности толщиною dx, будет равна .

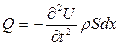Применяя третье начало Ньютона, можно записать

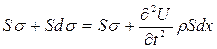
После приведенных подобных членов и сокращения на S получим

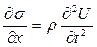(20.10)

Известно, что 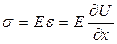,так что, находим

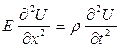
или

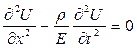(20.11)

Так как в соответствии с (20.9) 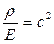, то окончательно получаем уравнение

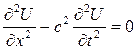, (20.12)

которое является однородным гиперболическим урав­нением второго порядка с постоянными коэффициентами, его решение имеет следующий вид:

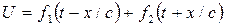(20.13)

где f ₁, f ₂ — произвольные функции своих аргументов (опреде­ляются начальными и граничными условиями).

Первый член в (20.13) соответствует распространению уп­ругой волны в положительном направлении оси отдельности, а второй — в отрицательном.

Аргументы функций (20.13) имеют размерность времени. При этом, как правило, принимается, что значения t - х/с (для f ₁) и t = - х/с (для f ₂) соответствуют передним фронтам волн, так что самим волнам соответствуют значения аргументов

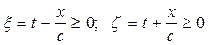
Рассмотрим распространение упругой волны напряжений сжатия вдоль отдельности в положительном направлении оси X, т.е. примем U = f ₁(ξ ). Величина деформации частиц породы, че­рез которые в данный момент проходит волна, определяется как

,

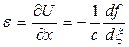напряжение

,

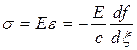при этом 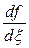>0.

Находим скорость частиц породы при прохождении по ним импульса напряжений:

.

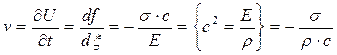Таким образом, можно считать, что этот импульс был гене­рирован в отдельности путем воздействия на него силой

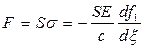
в некотором сечении DD ₁слева от сечения АВ и находящегося от него на расстоянии l = сτ, где τ — время, спустя которое им­пульс напряжений пришел в сечение АВ после действия на от­дельность силы F в сечении DD ₁.

Рассчитаем величину энергии в импульсе. Удельная потен­циальная энергия упругих деформаций частиц породы равна 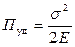, а удельная кинетическая энергия частицы 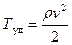. Учитывая (20.2) и (20.5), легко установить, что

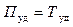(20.14)

Действительно,

.

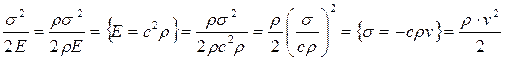При этом полная удельная энергия частиц в импульсе на­пряжений:

.

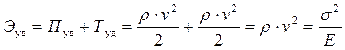Рассмотрим теперь отражение упругой волны сжатия от свободного торца отдельности, плоскость которого перпендику­лярна ее оси. Пусть имеет место рассмотренный выше случай распространения упругой волны напряжений в отдельности сле­ва направо вдоль положительной оси (рис. 20.2).

При этом для импульса сжатия, падающего на свободный торец отдельности ВВ, имеют место соотношения:

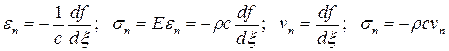. (20.15)

Этот импульс отразится от свободного конца ВВ ₁в виде нового импульса U ₀ = f ₂ (t + x/c) с параметрами σ ₀, ε ₀, v ₀ и будет распространяться по отдельности вдоль отрицательного направ­ления оси X. При этом будут иметь место соотношения:

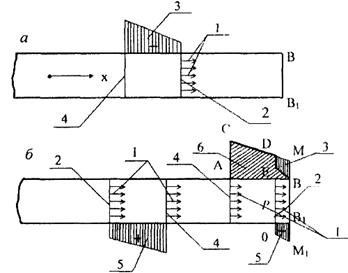
Рис. 20.2. Схема отражения плоской волны от свободной поверхности: а — импульс сжатия, падающий на торец отдельности ВВ; б— процесс отражения импульса сжатия от свободного торца ВВ] отдельности: / — направления скоростей частиц; 2 — пе­редний фронт уже отразившейся части импульса; 3 — эпюра ACDMB падающего импульса напряжений; 4 — концевой фронт напряжений; 5 — эпюра В\М\ОР отраженного импульса напряжений (растяжения); б — эпюра ACDEB результирующего импульса напряжений

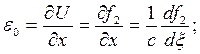(20.16)

.

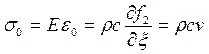Поскольку конец отдельности ВВ ₁свободен, то на нем при х = l полные напряжения и деформации равны нулю. Значит, в этом случае для построения отраженного импульса надо к концу стержня ВВ ₁приложить внешнее напряжение, равное по вели­чине и обратное по знаку тому, которое возникнет в сечении ВВ ₁, под действием падающего импульса, т.е. 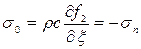, следовательно, .

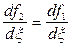При этом скорость частиц в отраженном импульсе

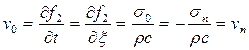(20.17)

Таким образом, в сечении ВВ ₁суммарные напряжения и де­формации будут равны нулю, а полная скорость частиц v_a = v ₀ + v_n = 2 v_n (см. рис. 20.2).

Рассмотренное выше явление отражения волны сжатия от свободного торца отдельности показывает, что в случае дейст­вия в отдельности импульса напряжения сжатия конечной дли­ны, меньшей, чем длина отдельности, от свободного торца от­дельности отражается импульс напряжения растяжения конеч­ной длины. Аналогичное явление — изменение знака у напря­жений и сохранение знака у скорости — имеет место и при па­дении на свободный торец отдельности импульса растяжения, так что общее правило следующее:

- при падении импульса на­пряжения на свободный торец отдельности у отраженного импульса направление скорости совпадает с направлением ско­рости в падающем импульсе, а знаки напряжений и деформаций в отраженном импульсе меняются на противоположные зна­кам этих, величин в падающем импульсе.

После полного отражения падающего импульса сжатия в отдельности будет распространяться только отраженный им­пульс растяжения (см. рис. 20.2, б). И если порода в отдель­ности имеет существенно разные пределы прочности на сжа­тие и на растяжение 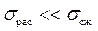, то отраженный импульс напряжения растяжения может вызвать разрушение, хотя им­пульс сжатия разрушения не вызывал. Подчеркнем, что для возникновения разрушения при совместном действии па­дающего и отраженного импульсов необходимо, чтобы на­пряжение растяжения в отраженном импульсе было больше по абсолютной величине напряжения сжатия в падающем импульсе, по крайней мере, на величину 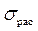так, чтобы суммарное напряжение от падающего и отраженного импульсов удовлетворяло условию 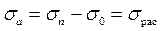. Рассмотрим отражение упругой волны от жестко закреплен­ного торца отдельности. Пусть по стержню распространяется импульс сжатия слева направо вдоль положительного направле­ния оси X. Для этого импульса выполняются соотношения (20.15). Дойдя до жестко закрепленного торца отдельности при х = l, импульс сжатия отразится в виде нового импульса с пара­метрами σ ₀, ε ₀, v ₀. Для которого имеют место соотношения (20.16).

Поскольку торец отдельности ВВ ₁жестко закреплен, при х=l суммарная скорость от падающего и отраженного импуль­сов должна быть равна нулю, то есть

v_a = v ₀ + v_n = 0 или v ₀ = - v_n (20.18)

При этом напряжение в отраженном импульсе будет опре­деляться по формулам

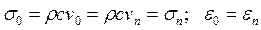. (20.19)

Аналогичное явление имеет место и при отражении импуль­са растяжения от жестко закрепленного торца. Так что общее правило в этом случае таково:

- при падении импульса напряже­ний на жестко закрепленный торец отдельности происходит отражение импульса, у которого знаки напряжений и дефор­маций совпадают со знаками этих величин в падающем импуль­се, а направление скоростей частиц в отраженном импульсе про­тивоположно направлению скоростей в падающем импульсе.

Рассмотрим процесс преломления и отражения импульса напряжения на плоскости контакта двух отдельностей с разны­ми площадями поперечных сечений и из разных материалов (рис. 20.3).

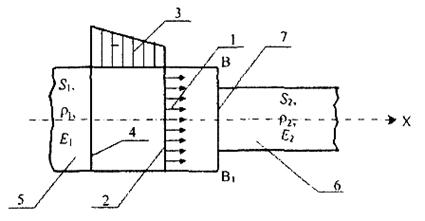
Рис. 20.3. Схема падения импульса напряжения на поверхность плотного контакта ВВ ₁, двух отдельностей:

1 — направления скоростей частиц в падающем импульсе; 2 — передний фронт; 3 — эпюра напряжений; 4 — концевой фронт; 5 — первая отдельность; 6 — вторая отдельность; 7 — плоскость плотного контакта двух отдельностей

Пусть в левой отдельности с параметрами S ₁; ρ ₁; Е ₁ распространяется слева направо импульс напряжений σ_n, ε_n, v_n к плоскости плотного контакта этой отдельности со второй от­дельностью с параметрами S ₂; ρ ₂; Е ₂.Примем, что плоскость их контакта перпендикулярна к осям обеих отдельностей. В мо­мент выхода импульса напряжений на плоскость плотного кон­такта ВВ ₁произойдет частичное преломление и частичное отражение падающего импульса. При этом вследствие различий площадей поперечных сечений отдельностей вблизи поверхно­сти контакта в обеих отдельностях будут формироваться слож­ные напряженно-деформированные состояния. Пренебрегая эти­ми процессами, в отдельностях около их контактирующих тор­цов будем считать, что и в рассматриваемом случае справедлива изложенная выше теория Сен-Венана. Полученные в этом случае результаты, за исключением концевых зон и начальных участ­ков прошедшего и отраженного импульсов, практически будут совпадать с точным решением, полученным на основе трехмер­ной волновой теории, если S ₁ существенно не отличается от S ₂.

Примем для определенности, что S ₁ > S ₂. Скорости частиц в прошедшем импульсе будут направлены в ту же сторону, что и в падающем импульсе, а напряжение и деформации сжимающие, т.е. v ₂ > 0; σ ₂ < 0; ε ₂ < 0. Примем, что и в отраженном импульсе в первой отдельности скорости частиц направлены вправо, т.е. v _1,0 > 0. При этом в соответствии с рассмотренной выше задачей и принятым допущением (S ₁ > S ₂)будем считать, что в отражен­ном импульсе напряжения и деформации будут растягивающи­ми, т.е. σ _1,0 > 0; ε _1,0 > 0. На плоскости плотного контакта отдель­ностей будет выполняться одно кинематическое условие — ра­венство абсолютных скоростей смещения частиц и одно дина­мическое условие — равенство сил.

Учитывая сделанные выше замечания, математически оба усло­вия записываются в виде

v ₂ = v _1,0 + v _{1, n} = 0; (19.20)

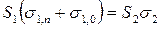. (19.21)

Учитывая (19.12), условие (19.16) преобразуется к виду

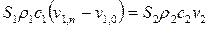(19.22)

Произведения 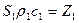и 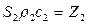принято называть импедансами. Из (19.19) и (19.21) простыми преобразованиями находим

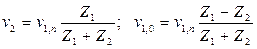(19.23)

Из соотношений (19.23) следует, что если Z ₁ = Z₂, то весь импульс напряжений из первой отдельности проходит во вто­рую, причем скорость частиц v ₂ в прошедшем импульсе будет равна v _{1, n}.

Если же Z ₁ > Z₂, то во вторую отдельность проходит только часть падающего импульса, при этом отраженный импульс в первой отдельности будет импульсом растяжения, поскольку в этом случае v _1,0 > 0, a v₂ будет больше v _{1, n}.

В случае, если Z ₁ < Z₂, то во вторую отдельность также бу­дет проходить не весь импульс, а только часть его, при этом в первую отдельность от плоскости контакта BB ₁ будет отражать­ся импульс сжатия (v _1,0 < 0), а v ₂ будет меньше v _{1, n}.

Рассчитаем полную энергию в прошедшем и отраженном импульсах за время dt действия падающего импульса.

Полная энергия в прошедшем импульсе:

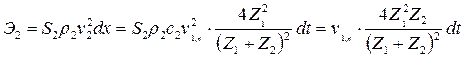. (19.24)

Полная энергия в отраженном импульсе:

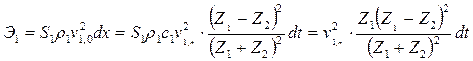. (19.25)

Сумма энергий:

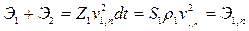(19.26)

где Э_{1, n} — полная энергия падающего импульса в первой от­дельности.

Соотношением (19.26) подтвержден закон сохранения энергии.

Рассмотренные решения для плоских упругих волн малой амплитуды выявили для них следующие свойства:

• все параметры волны — скорость частиц v, давление р,
плотность ρ, температура Т — однозначно выражаются друг
через друга. Так что если удалось каким-то образом найти
один из них, то по соответствующим формулам рассчитываются и все другие;

• амплитуда и форма плоских упругих волн малой амплитуды с течением времени, т.е. по мере их распространения по
отдельности, не изменяются. Действительно, упругие волны,
определяемые решениям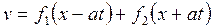и

и ,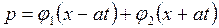

не изменяются с течением времени t no мере их распространения по отдельностям;

• скорость распространения продольных упругих волн малой амплитуды постоянна.