Теорема Безу. Схема Горнера
Определение 1.2.1. Полиномом степени n называется сумма
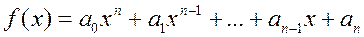 ,
,
где 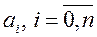 — комплексные числа,
— комплексные числа, 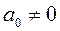 ,
,
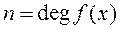 — степень полинома
— степень полинома 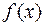 .
.
Если 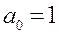 , то полином называется приведенным.
, то полином называется приведенным.
Определение 1.2.2. Два полинома
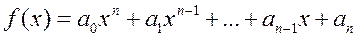 ,
, 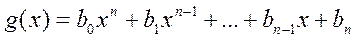
называются равными, если для любого 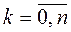 справедливы равенства
справедливы равенства
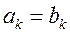 .
.
Теорема 1.2.1. Для любых двух полиномов 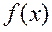 и
и 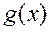 ,
, 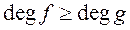 , существуют такие однозначно определяемые полиномы
, существуют такие однозначно определяемые полиномы 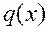 и
и 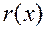 , что
, что
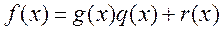 , (1.2.1)
, (1.2.1)
причем 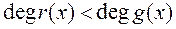 , либо
, либо 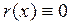 .
.
Доказательство. Пусть
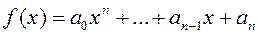 ,
, 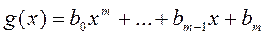 ,
,
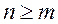 ,
,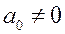 ,
, 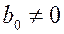 .
.
Построим вспомогательный полином
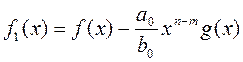 . (1.2.2)
. (1.2.2)
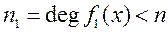 ,
, 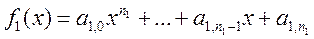 .
.
Если 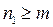 , то строим следующий полином
, то строим следующий полином
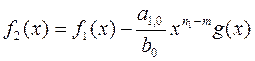 , (1.2.3)
, (1.2.3)
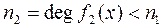 , причем
, причем 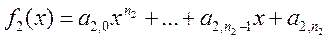 .
.
Если 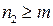 , то находим другой полином
, то находим другой полином
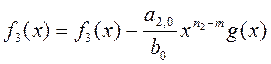 , (1.2.4)
, (1.2.4)
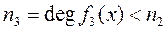 и т. д.
и т. д.
По построению 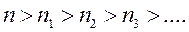
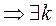 , что
, что
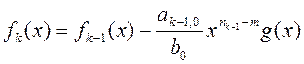 , (1.2.5)
, (1.2.5)
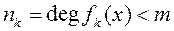 .
.
Складывая (1.2.2) + (1.2.3) + (1.2.4) +…+ (1.2.5), получаем слева полином
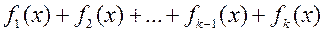 ,
,
а справа —
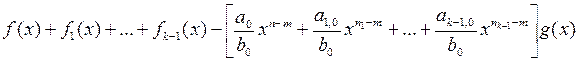 .
.
После сокращений
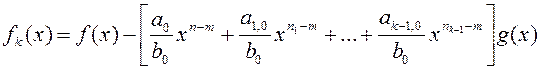 ,
,
поэтому, если
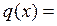
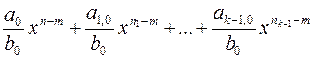 ,
, 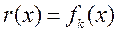 ,
,
то получаем равенство (1.2.1).
Докажем теперь, что полиномы 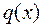 и
и 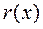 определяются однозначно. Предположим, что
определяются однозначно. Предположим, что
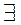
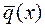 и
и 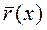 :
: 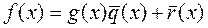 ,
,
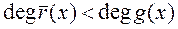 (или
(или 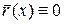 ).
).
Тогда
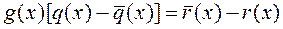 .
.
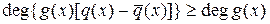 ,
, 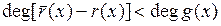
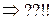
Определение 1.2.3. Полином 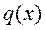 называется частным, а
называется частным, а 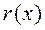 — остатком от деления полинома
— остатком от деления полинома 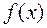 на полином
на полином 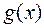 .
.
Определение 1.2.4. Если 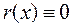 , то говорят, что полином
, то говорят, что полином 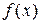 делится нацело на полином
делится нацело на полином 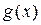 (обозначение
(обозначение 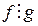 ), а сам полином
), а сам полином 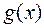 при этом называется делителем полинома
при этом называется делителем полинома 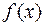 .
.
Теорема 1.2.2 (теорема Безу). Полином 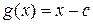 является делителем полинома
является делителем полинома 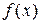 тогда и только тогда, когда
тогда и только тогда, когда 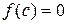 .
.
Доказательство. Необходимость. Если
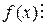
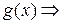
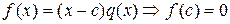
Достаточность. Пусть 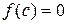 . Из формулы (1.2.1) имеем соотношение
. Из формулы (1.2.1) имеем соотношение
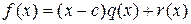 ,
,
причем 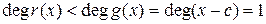 .
.
Следовательно, 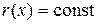 , тогда
, тогда 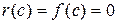 , отсюда
, отсюда 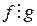 .
.
Следствие 1.2.1. Остаток от деления полинома 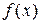 на полином
на полином 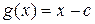 равен
равен 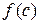 .
.
Доказательство.
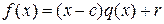 ,
,
где 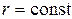 . Подставляя
. Подставляя 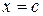 ,получаем
,получаем 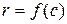 , что и требовалось доказать.
, что и требовалось доказать.
Возьмем произвольно полином 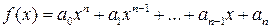 . Пусть
. Пусть 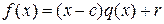 , где
, где 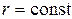 . Ясно, что
. Ясно, что 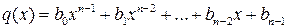 .
.
Для определения остатка r и коэффициентов 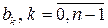 имеем очевидное соотношение
имеем очевидное соотношение
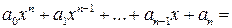
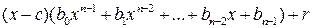 .
.
Сравнивая коэффициенты полиномов при одинаковых степенях x, имеем
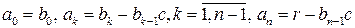 ,
,
поэтому окончательно получаем
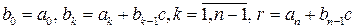 . (1.2.6)
. (1.2.6)
Формулы (1.2.6) носят название схемы Горнера.
Определение 1.2.5. Корнем полинома 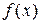 называется число c, такое что
называется число c, такое что 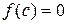 .
.
Пусть 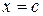 — корень полинома
— корень полинома 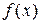 . Тогда
. Тогда
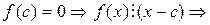
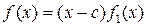 .
.
Если 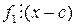 , то
, то 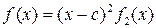 .
.
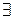 k:
k: 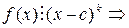
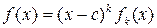 ,
, 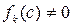 .
.
Определение 1.2.6. Указанное число k называется кратностью корня 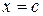 полинома
полинома 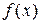 . Если
. Если 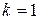 , то соответствующий корень называется простым, а при
, то соответствующий корень называется простым, а при 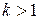 — кратным.
— кратным.
Определение 1.3.1. Алгебраическим уравнением n-й степени одной переменной x называется уравнение вида
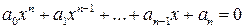 ,
,
где 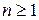 ,
, 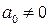 ,
, 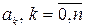 — комплексные числа.
— комплексные числа.
Теорема 1.3.1 (основная теорема высшей алгебры). Любое алгебраическое уравнение имеет, по крайней мере, один корень (вещественный или комплексный).
Доказательство теоремы приведено, например, в учебнике А.Г.Куроша «Курс высшей алгебры».
Теорема 1.3.2. Любой полином 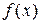 ,
, 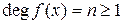 , с любыми числовыми коэффициентами имеет ровно n корней, если каждый корень считать столько раз какова его кратность.
, с любыми числовыми коэффициентами имеет ровно n корней, если каждый корень считать столько раз какова его кратность.
Доказательство. Пусть 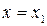 является корнем полинома
является корнем полинома 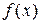 .
.
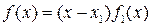 ,
,
где 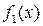 — полином степени n – 1.
— полином степени n – 1.
Если 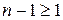 , то
, то 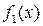 имеет хотя бы один корень, например,
имеет хотя бы один корень, например, 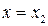 .
.
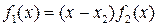
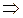
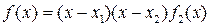 .
.
Продолжая подобные рассуждения, получаем,
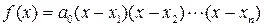 .
.
Все числа 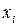 ,
, 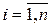 , являются корнями полинома
, являются корнями полинома 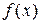 , так как для любого
, так как для любого 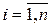 справедливо равенство
справедливо равенство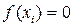 .
.
Докажем теперь, что разложение полинома 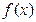 на множители определяется однозначно с точностью до порядка сомножителей. Доказательство этого факта проведем от противного.
на множители определяется однозначно с точностью до порядка сомножителей. Доказательство этого факта проведем от противного.
Пусть существует другое разложение полинома 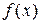 на множители, т. е.
на множители, т. е. 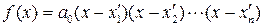 . Допустим, что среди корней
. Допустим, что среди корней 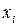 ,
, 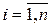 , существует такой корень
, существует такой корень 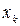 , что
, что 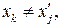 для любого
для любого 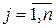 . Подставляя
. Подставляя 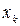 в очевидное равенство
в очевидное равенство
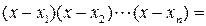
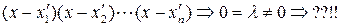
Таким образом, для любого 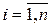 существует такое
существует такое 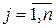 , что
, что 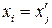 . Однако, из этого еще не следует, что разложение полинома
. Однако, из этого еще не следует, что разложение полинома 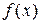 на множители определяется однозначно, так как корни
на множители определяется однозначно, так как корни 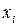 для различных
для различных 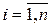 могут совпадать.
могут совпадать.
Допустим, что среди корней 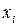 существует ровно
существует ровно 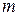 , равных
, равных 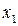 , в то время как среди корней
, в то время как среди корней 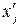 имеется только
имеется только 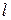 , равных
, равных 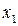 .
.
Предположим, что 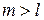 . Приравнивая различные разложения полинома
. Приравнивая различные разложения полинома 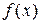 , получаем равенство
, получаем равенство 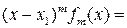
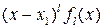 , причем
, причем 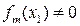 ,
, 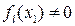 .
.
Сокращая обе части этого соотношения на общий множитель 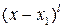 , получаем
, получаем 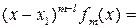
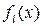 . Заметим, что при подстановке в последнее равенство
. Заметим, что при подстановке в последнее равенство 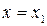 левая часть обращается в нуль, в то время как правая отлична от нуля. Отсюда следует, что
левая часть обращается в нуль, в то время как правая отлична от нуля. Отсюда следует, что 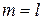 .
.
Если объединить сомножители, отвечающие совпадающим корням, то полином
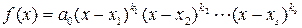 ,
,
где 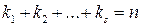 , а
, а 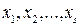 — различные корни полинома
— различные корни полинома 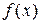 .
.
Таким образом, полином степени n не может иметь более чем n корней.
Теорема 1.3.3. Если полиномы 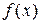 ,
, 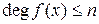 и
и 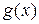 ,
, 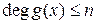 имеют совпадающие значения в более чем
имеют совпадающие значения в более чем 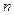 различных точках, то
различных точках, то
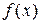 =
=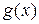 .
.
Доказательство. Рассмотрим полином 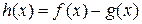 . Очевидно, что
. Очевидно, что 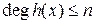 . Но по условию теоремы полином
. Но по условию теоремы полином 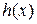 обращается в нуль в более чем
обращается в нуль в более чем 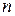 различных точках. Однако у этого полинома не может быть корней больше чем
различных точках. Однако у этого полинома не может быть корней больше чем 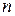 . Поэтому
. Поэтому 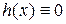 , т. е.
, т. е. 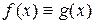 .
.
 2014-02-09
2014-02-09 1908
1908







