Поле интегрирования

Откуда

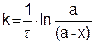или 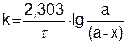(5.13)

Это уравнение дает возможность вычислить концентрацию реагирующего вещества в любой момент времени по известной величине константы скорости, или найти константу скорости реакции при заданной температуре путем определения концентрации в любой момент времени.

Из уравнения (5.13) следует, что размерность константы скорости реакции первого порядка будет t^-1 (например, мин^-1 или с ^-1).

Скорость реакции первого порядка не зависит от объема (разбавления), в котором протекает реакция. Иными словами, в единицу времени превращению подвергается одна и та же часть вещества.

Наряду с константой скорости, реакции характеризуют периодом полураспада (t_1/2) – временем, за которое прореагировало половина вещества:

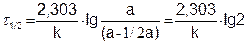(5.14)

Из уравнения (5.14) следует, что константа скорости реакции первого порядка обратно пропорциональна периоду полураспада.

По закону реакций первого порядка протекают в основном физические процессы: диффузия, растворение, радиоактивный распад; и некоторые химические реакции: гидролиз полисахаридов и т.д.

К реакциям второго порядка относятся реакции соединения типа А + В → С или обмена А + В → С + D, а так же реакции разложения и др. Скорость реакции второго порядка определяется уравнением:

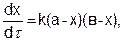(5.15)

где k – константа скорости, a и b – число молей веществ А и В в начальный момент времени, х – число прореагировавших молей.

Здесь возможны два случая. Первый случай, когда вещества а и b вступают в реакцию в эквивалентных количествах (a = в) и второй, когда (a ≠ в). Рассмотрим оба случая.

Первый случай (a = в). Уравнение (5.15) принимает вид

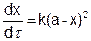(5.16)

Разделяя переменные и проводя интегрирование, получим

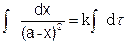(5.17)

Откуда

1/(а – х) = kt + const. (5.18)

При t = 0, x = 0

const = 1/а (5.19)

Подставив уравнения (5.19) в (5.18), получим

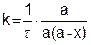(5.20)

Размерность константы скорости реакции первого порядка [мин^-1(моль/дм³)^-1]. В данном случае скорость реакции зависит от разбавления раствора или его концентрации.

Второй случай (a ≠ в). Если для реакции взяты неэквивалентные количества реагирующих веществ, то

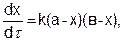(5.21)

После разделения переменных получим это уравнение в другом виде:

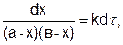(5.22)

Выражение, стоящее в левой части уравнение (5.22), можно представить как

.

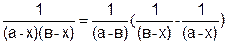После подстановки этого выражения в уравнение (5.22) получим

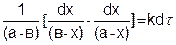(5.23)

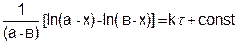(5.24)

Поскольку при t = 0, x = 0, постоянная интегрирования равна

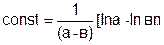(5.25)

Таким образом, подставляя это выражение в уравнение (5.24), найдем

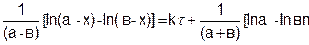
Откуда

k = 1/t • 2,303/(а – в)[ln(в(а – х)/а(в – х)] (5.26)

Это и есть кинетическое уравнение реакции второго порядка при условии (a ≠ в).

Определить, какого порядка данная реакция можно, используя метод подстановки. Для этого из реакционной смеси отбирают пробы через определенный промежуток времени и анализируют на содержание исходных веществ. Затем полученные значения подставляют в кинетические уравнения первого или второго порядка. И тем уравнением, где константа скорости в ходе процесса не меняется, определяется и порядок реакции.