Случайная величина – это величина (число), которая в результате опыта может принимать то или иное значение.
Более строго, случайная величина – это числовая функция случайного события. 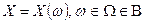
Случайная величина называется дискретной, если множество ее значений конечно или счетно. Здесь 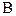 - алгебра событий. Например, число очков на грани брошенной кости, число бросков монеты до появления герба – дискретные случайные величины.
- алгебра событий. Например, число очков на грани брошенной кости, число бросков монеты до появления герба – дискретные случайные величины.
Случайная величина называется непрерывной, если ее значения заполняют некоторый интервал, возможно, бесконечный. Здесь 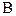 - сигма - алгебра событий. Например, расстояние от центра мишени при стрельбе, время до отказа прибора, ошибка измерения – непрерывные случайные величины.
- сигма - алгебра событий. Например, расстояние от центра мишени при стрельбе, время до отказа прибора, ошибка измерения – непрерывные случайные величины.
Рассмотрим дискретную случайную величину, принимающую значения 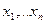 . Имеем полную группу (иначе, не все значения учтены) несовместных событий
. Имеем полную группу (иначе, не все значения учтены) несовместных событий 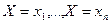 . Вероятности этих событий равны соответственно
. Вероятности этих событий равны соответственно 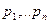
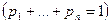 . Будем говорить, что дискретная случайная величина
. Будем говорить, что дискретная случайная величина 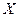 принимает значения
принимает значения 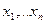 с вероятностями
с вероятностями 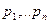 .
.
Законом распределения дискретной случайнойвеличины называется любое соотношение, устанавливающее зависимость между ее значениями 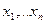 и вероятностями
и вероятностями 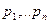 , с которыми эти значения достигаются.
, с которыми эти значения достигаются.
Основные формы закона распределения дискретной случайной величины: ряд распределения – таблица
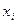 | 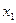 | ….. 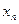 |
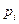 | 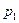 | …..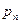 |
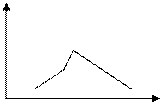
 многоугольник распределения
многоугольник распределения
p3
p2
p1, pn
x1 x2 x3 …xn
Можно задать закон распределения в виде аналитической зависимости, связывающей значения 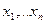 и вероятности
и вероятности 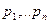 .
.
Рассмотрим непрерывную случайную величину. Для непрерывной случайной величины 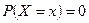 , поэтому рассматривают события
, поэтому рассматривают события 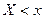 и вероятности этих событий.
и вероятности этих событий.
Функцией распределения непрерывной случайной величины 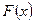 называется вероятность события
называется вероятность события 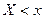 .
. 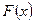 =
=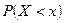 .
.
 2014-02-12
2014-02-12 871
871








