Напомним, что опытом в теории вероятностей называют контролируемое осуществление некоторого комплекса условий S, которое можно повторить неограниченное число раз. Пусть производится n опытов (испытаний), в каждом из которых может наступить один из N исходов. Определение 1. Если результаты одного испытания не зависят от результатов других испытаний, то такие испытания называются независимыми.
Пример. В урне 3 белых и 4 чёрных шара. Вынимают 2 шара по очереди. Событие А – вытащить 1й шар белый B и второй белый. Событие В – вытащить 2й шар белый. Покажем, что события А и В зависимы. 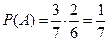 ,
, 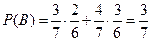 ,
, 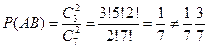 .
.
Возможны две ситуации: условия проведения испытаний не меняются (ситуация А) или меняются от испытания к испытанию (ситуация В).
Определение 2. Схема независимых испытаний с неизменными условиями и с двумя исходами в каждом из которых некоторое случайное событие А наступает с одной и той же вероятностью p = P(A), не изменяющейся от испытания к испытанию, называется схемой Бернулли.
Схема Бернулли отвечает на следующие группы вопросов:
I. Какова вероятность того, что в серии из 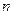 независимых испытаний событие
независимых испытаний событие 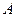 появится ровно
появится ровно 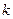 раз. В этом случае любой исход n испытаний Бернулли представляет собой последовательность длины n, состоящую из k "успехов" и (n – k) "неуспехов". Вероятность каждого такого исхода по теореме умножения независимых случайных событий равна pk(1 - p)n-k или pkqn-k, где q=1 - p. Число таких комбинаций равно числу способов выбора k мест из n для "успеха". Тогда
раз. В этом случае любой исход n испытаний Бернулли представляет собой последовательность длины n, состоящую из k "успехов" и (n – k) "неуспехов". Вероятность каждого такого исхода по теореме умножения независимых случайных событий равна pk(1 - p)n-k или pkqn-k, где q=1 - p. Число таких комбинаций равно числу способов выбора k мест из n для "успеха". Тогда 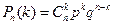
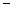 формула Бернулли.
формула Бернулли.
Пример. Какова вероятность с пяти раз вытащить из колоды в 36 карт ровно три туза? Карты каждый раз возвращаются в колоду. 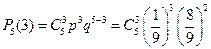
Пример. Что вероятнее: выиграть у равносильного противника в шахматы 2 партии из трех или 3 партии из четырех? Р3(2)= 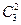 (1/2)2(1/2) = 3/8, Р4(3) =
(1/2)2(1/2) = 3/8, Р4(3) = 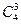 (1/2)3(1/2) = 1/4. То есть вероятнее выиграть 2 партии из трех.
(1/2)3(1/2) = 1/4. То есть вероятнее выиграть 2 партии из трех.
Приближения. При большом числе n повторных испытаний использование формулы Бернулли затруднительно в связи с необходимостью выполнения действий над очень большими числами.
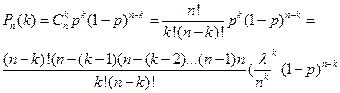
 2014-02-12
2014-02-12 972
972








