Для дискретной случайной величины 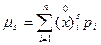 .
.
Для непрерывной случайной величины 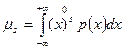 .
. 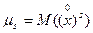
Дисперсией называется второй центральный момент случайной величины. 
По свойствам математического ожидания получим 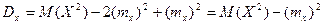 . Эта формула часто применяется. Дисперсия – это характеристика рассеяния, она характеризует концентрацию кривой распределения (графика плотности распределения) около математического ожидания. Если на числовой оси расположить точки xi с массами pi, то дисперсия – это момент инерции системы материальных точек относительно центра тяжести mx.
. Эта формула часто применяется. Дисперсия – это характеристика рассеяния, она характеризует концентрацию кривой распределения (графика плотности распределения) около математического ожидания. Если на числовой оси расположить точки xi с массами pi, то дисперсия – это момент инерции системы материальных точек относительно центра тяжести mx.
Для дискретных случайных величин  .
.
Для непрерывных случайных величин 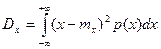 .
.
 2014-02-12
2014-02-12 378
378








