2014-02-12
410
Числовые характеристики случайных величин.
Свойства плотности распределения.
1) 
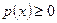, так как функция распределения – неубывающая функция,
2) 
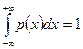(условие нормировки), так как 
.
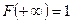Для дискретных случайных величин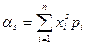 
.
Для непрерывных случайных величин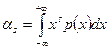 
.
Математическим ожиданием случайной величины называется ее первый начальный момент mx = M(x) =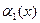 
.
Для дискретных случайных величин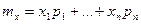 
. Если на числовой оси расположить точки 
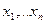с массами 
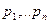, то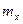 
- абсцисса центра тяжести системы точек. Аналогично, для непрерывных случайных величин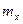 
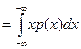имеет смысл центра тяжести кривой распределения.
