Распределения, связанные с повторными испытаниями.
Рассмотрим схему Бернулли. Обозначим Х – число испытаний до первого успеха, если вероятность успеха в одном испытании р. Если первое испытание успешно, то Х = 0. Следовательно, 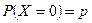 . Если Х = 1, т.е. первое испытание неудачно, а второе успешно, то по теореме умножения
. Если Х = 1, т.е. первое испытание неудачно, а второе успешно, то по теореме умножения 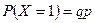 . Аналогично, если Х = n, то все испытания до n-ого неудачны и
. Аналогично, если Х = n, то все испытания до n-ого неудачны и 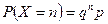 . Составим ряд распределения случайной величины Х
. Составим ряд распределения случайной величины Х
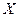
| … | 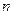
| … | |||
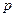
| 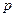
| 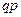
| 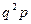
| … | 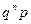
| … |
Случайная величина с таким рядом распределения имеет геометрическое распределение.
Проверим условие нормировки 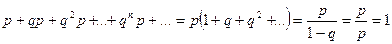 .
.
 2014-02-12
2014-02-12 452
452








