2014-02-12
1243
В ряде задач требуется не только найти с помощью статистических данных точечную оценку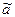 
для параметра 
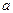распределения, но и оценить ее точность и надежность, так как в силу случайности 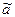приближенная заме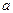на на 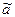может привести к серьезным ошибкам. Для точности оценки в математической статистике используют доверительные интервалы.
Пусть для параметра 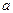распределения случайной величины Х получена несмещенная оценка 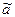. Задаем достаточно высокую вероятность 
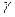(например, 
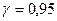) и находим такое значение e > 0, для которого
.
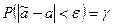Равенство можно переписать в другом виде
.
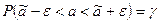Последнее равенство можно истолковать следующим образом: неизвестное значение параметра а с вероятностью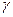 
попадает в интервал 
.
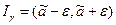Но так как неизвестное значение параметра 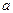является неслучайной величиной, оценка 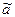этого параметра – случайной, то равенство можно истолковать более точно следующим образом: интервал 
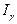с высокой вероятностью 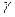покрывает неизвестный параметр .
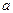Интервал 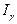называется доверительным интервалом; центр его находится в точке 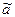, радиус его e. Вероятность 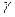называется доверительной вероятностью или надежностью.
Итак, доверительный интервал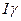 
– это интервал с центром в точке 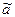и радиусом e, который с высокой вероятностью (надежностью) покрывает неизвестный параметр
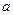. Найти доверительный интервал – это значит по статистическим данным найти центр интервала 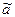и радиус его e> 0.
